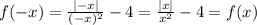
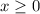, поэтому она не может быть четной или нечетной. Для этого требуется симметрия области определения относительно нуля.
Я не давно решала на уроке это уравнение, твоё решить сложно..., Попробуй решить своё на этом же примере...
Пошаговое объяснение:
Задание:
Напишите уравнение касательной к графику функции у=f(x)в точке, абсцисса которой равна х0:f(x)=4x2+x-1,x0=2
Уравнение касательной, проведенной к графику функции y=f(x) в точке x0, имеет вид: y=f(x0)+ f'(x0)(x-x0), где f(x0) - значение функции f(x) в точке х0, f'(x0) - значение производной данной функции в точке х0.
1) Найдем значение функции f(x) в точке х0: f(x0)=4(х0)^2+x0-1=4*(2)^2+2-1=4*4+2-1=17;
2) Найдем производную функции f(x): f'(x)=4*2*x+1=8x+1;
3) Найдем значение производной f'(x) в точке х0: f'(x0)=8*х0+1=8*2+1=17;
4) Подставим найденные значения f(x0) и f'(x0) в уравнение касательной: y=f(x0)+ f'(x0)(x-x0) = 17+17*(х-2) = 17+17х-34 = 17х-17.
300/100*12=36
Пошаговое объяснение: