Пошаговое объяснение:
при х≥0 IxI=x
y=x(x-4)-6x=x²-4x-6x=x²-10x
при х<0 IxI=-x
y=-x(x-4)-6x=-x²+4x-6x=-x²-2x
найдем точки пересечения графиков x²-10x=-x²-2x; 2x²-8x=0; 2x(x-4)=0
x1=0;x2=4
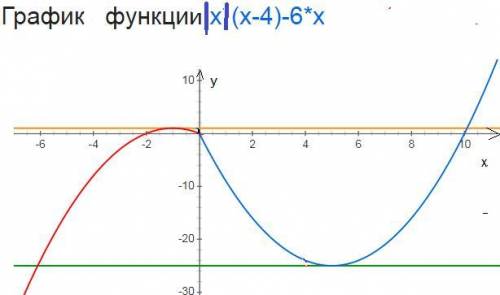
y=x²-10x это парабола, вершина х0=-b/2a=10/2=5; y0=25-50=-25
вершина (5;-25) точки пересечения с осью ОХ x(x-10)=0; x1=0;x2=10
y=-x²-2x это парабола, вершина х0=-b/2a=-2/2=-1; y0=-1+2=1
вершина (-1;-1) точки пересечения с осью ОХ -x(x+2)=0; x1=0;x2=-2
из графика видно что прямая у=к будет иметь с графиком ровно две общие точки если будет проходить через вершины
у=1; y=-25
⇒ k={1;-25}
б)2/5<x<3/5⇒8/20<x<12/20⇒x=9/20,10/20,11/20 или х=9/20,1/2,11/20
в)1/3<x<1/2⇒8/24<x<12/24⇒x=9/24,10/24,11/24 или х=3/8,5/12,11/24
a)9/10<x<1⇒36/40<x<40/40⇒x=37/40,38/40,39/40 или х=37/40,19/20,39/40
б)3/7<x<4/7⇒12/24<x<16/28⇒x=13/24,14/28,15/28 или х=13/24,7/14,15/28
в)1/4<x<1/3⇒15/60<x<20/60⇒x=16/60,17/60,18/60 или х=4/15,17/60,3/10