Question

Решите эти уравнения с полным обьяснением
6) 1,2(x − 4) + 4,6 = 0,3(3 + x)
7) -0,6(x − 3) − 3,3 = 0,6(4 − x)
8) 11x + 15 = 7x − 25
9) 16x − 28 = 8x − 44
10) 4x − 15 = - 7( 9 + x)
11) 17x − 8 = 20x + 9
12) 21x + 24 = 34x + 3
13) 1,6(x − 2) + 3,4 = 0,7(4 + x)
14) -0,3(x − 9) − 4,8 = 0,3(5 − x)
15 )7y – 7=2y + 8

Answer 1

Слушай, а ты не оболдел столько номеров, за столбко давать?

Пошаговое объяснение:

6) 1,2(x - 4) + 4,6 = 0,3(3 + x)

Раскрываем скобки методом "фонтанчика"

1,2x - 4,8 + 4,6 = 0,9 + 0,3x

Переносим всё с x в левую часть, а всё остальное в правую (с изменением знака):

1,2x - 0,3x = 4,8 - 4,6 + 0,9

0,9x = 1,1

Домножаем на 10:

9x = 11

x =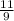 $\frac{11}{9}$

x =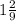 $1\frac{2}{9}$

Остальные аналогично.

7) -0,6(x - 3) - 3,3 = 0,6(4 - x)

-0,6x + 1,8 - 3,3 = 2,4 - 0,6x

-0,6x + 0,6x = 2,4 - 1,8 + 3,3

0 ≠ 3,9

Нет решения.

8) 11x + 15 = 7x - 25

4x = - 40

x = - 10

9) 16x - 28 = 8x - 44

16x - 8x = - 44 + 28

8x = - 16

x = - 2

10) 4x - 15 = - 7(9 + x)

4x - 15 = - 63 - 7x

11x = 48

x =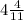 $4 \frac{4}{11}$

11) 17x - 8 = 20x + 9

17x - 8 - 20x - 9 = 0

- 3x - 17 = 0

- 3x = 17

x =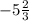 $-5\frac{2}{3}$

12) 21x + 24 = 34x + 3

21x - 34x = 3 - 24

- 13x = - 21

x =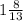 $1 \frac{8}{13}$

13) 1,6(x - 2) + 3,4 = 0,7(4 + x)

1,6x - 3,2 + 3,4 = 2,8 + 0,7x

1,6x + 0,2 - 2,8 - 0,7x = 0

0,9x = 2,6

9x = 26

x =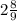 $2\frac{8}{9}$

14) - 0,3(x - 9) - 4,8 = 0,3(5 - x)

- 0,3x + 2,7 - 4,8 = 1,5 - 0,3x

- 0,3x + 0,3x = 1,5 - 2,7 + 4,8

0 ≠ 3,6

Нет решения.

15) 7y - 7 = 2y + 8

7y - 2y = 8 + 7

5y = 15

y = 3