Существует выбрать 9 клеток доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
Пошаговое объяснение:
Укажите сколькими можно выбрать 9 клеток на доске
9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
Вспомним как выглядит доска судоку ( рис. 1 во вложении ).
Вся задача сводится к тому , что надо определить сколькими можно разместить цифру в одной клетке , в каждом квадратике 3 х 3 соблюдая условие , что в каждом столбце и каждой строчке будет только одна цифра .
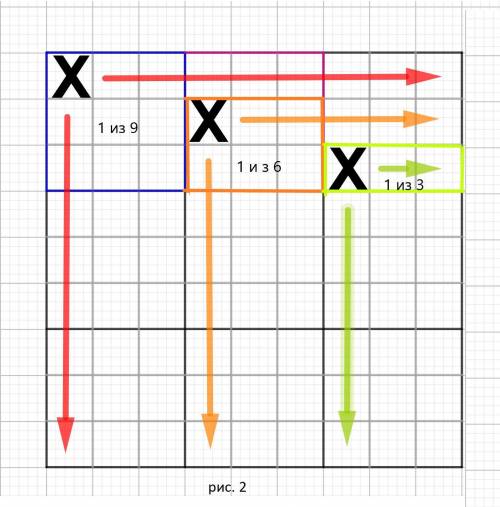
Берем первый сверху ряд .
Пусть первая цифра будет стоять в левом верхнем квадрате . В квадрате 9 клеток , надо выбрать одну , значит у нас будет
выбрать эту клетку .
В следующем квадрате 3 х 3 одна строка у нас уже занята , значит 3 клетки мы не можем выбрать , остается 9-3 = 6 клеточек для выбора . Получаем :
выбрать одну клетку .
Переходим в следующий квадрат 3 х 3 . В нем у нас уже две строки заняты , значит мы не можем выбрать :
3 * 2 = 6 клеток , остается
9 - 6 = 3 клетки для выбора . Получаем :
выбрать одну клетку.
Для наглядности изобразим это на рисунке 2 ( во вложении).
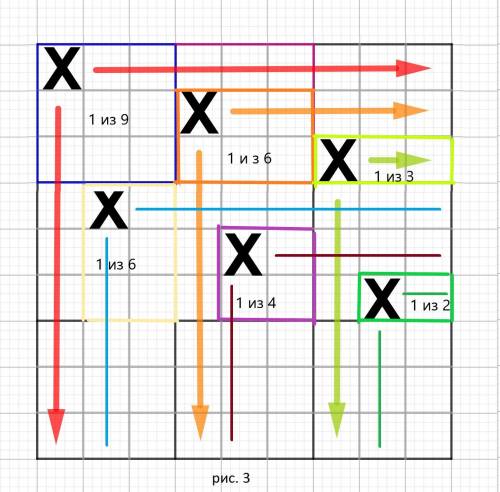
Берем второй ряд.
В первом слева квадрате ( рис. 3 во вложении) у нас 3 клетки заняты , значит остается : 9 - 3 = 6 клеток для выбора . Получаем :
выбрать 1 клетку
В следующем квадрате заняты уже 5 клеток ( рис. 3) , остается :
9 - 5 = 4 клетки для выбора . Получаем :
выбрать 1 клетку
В последнем квадрате занято 7 клеток , остается :
9 - 7 = 2 клетки для выбора . Получаем :
выбрать 1 клетку .
Отметим это все на нашем рисунке 3 ( во вложении) .
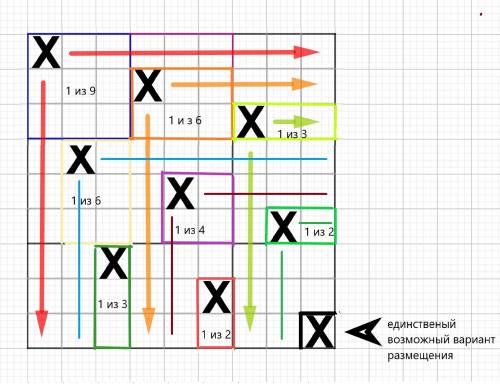
Переходим к последнему ряду , третьему .
В первом квадрате занято 6 клеток , остается 9 - 6 = 3 клетки для выбора . Получаем :
выбрать 1 клетку
Во втором квадрате занято 7 клеток, остается : 9 - 7 = 2 клетки для выбора и получаем :
выбрать 1 клетку.
В третьем , последнем квадрате нашей доски , свободный остается 1 квадрат , получаем :
1 * 1 = 1 единственный выбора клетки.
Отмечаем на рисунке 4 ( во вложении)
Мы выбрали 9 клеток , соблюдая условие задачи.
Теперь найдем сколькими можно выбрать 9 клеток доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
По правилу умножения :
.
Существует выбрать 9 клеток доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.

1) -3 + (-7) = -3 -7 = -10
2) -3 -7 = -10
3) -3 + 7 = 7 - 3 = 4
4) -3 - (-7) = (так как - на - даёт + то) = -3 + 7 = 7 - 3 = 4
5) -(-3) -(-7) = 3 + 7 = 10 (опять же - на - даёт плюс)
6) -(-3) + 7 = 3 + 7 = 10
7) -(-3) + (-7) = 3 - 7 = -4
8) -(-3) - 7 = 3 - 7 = - 4
9) 3 - 7 = -4
10) 3 + 7 = 10
11) 3 - (-7) = 3 + 7 = 10
12) 3 + (-7) = 3 - 7 = -4
a) -27 + 49 = 22
б) -27 + (-49) = -76 (по принципу: -1 -3 = -4)
в) -27 -49 = -76
г) 27 - 49 = -22
д) 27 + (-49) = 27 - 49 = -22
е) -(-27) -(-49) = 27 + 49 = 76
ж) -(-27) -49 = 27 - 49 = -22
з) -(-27) + 49 = 27 + 49 = 76
и) -(-27) + (-49)
к) -6 + (-0,6) = -6 - 0,6 = -6,6
л) 3,6 + (-2,4) = 3,6 - 2,4 = 1,2
м) -1,26 + 1,26 = 0
И в следующие разы загружай фотку нормально!
Пусть tg x = t, тогда получаем:
\sqrt{3}t- \sqrt{3}\cdot \frac{1}{t} =2
3
t−
3
⋅
t
1
=2
дальше решаем уравнение(домножаем на t обе части уравнения)
\begin{lgathered}t^2 \sqrt{3}-2t- \sqrt{3}=0\\ D=b^2-4ac=(-2)^2-4\cdot \sqrt{3}\cdot(- \sqrt{3})=4+12=16\\ \sqrt{D} =4\\ t_1= \frac{-b+ \sqrt{D} }{2a} = \frac{2+4}{2 \sqrt{3}} = \sqrt{3}\\ t_2=\frac{-b- \sqrt{D} }{2a} = \frac{2-4}{2 \sqrt{3}} =- \frac{1}{\sqrt{3}}\end{lgathered}
t
2
3
−2t−
3
=0
D=b
2
−4ac=(−2)
2
−4⋅
3
⋅(−
3
)=4+12=16
D
=4
t
1
=
2a
−b+
D
=
2
3
2+4
=
3
t
2
=
2a
−b−
D
=
2
3
2−4
=−
3
1
Возвращаемся к замене
\begin{lgathered}tg x = \sqrt{3}\\ x=arctg(\sqrt{3})+\pi n,n \in Z\\ x= \frac{\pi}{3} +\pi n,n \in Z\\ \\ tg x = - \frac{1}{\sqrt{3}} \\ x=arctg(- \frac{1}{\sqrt{3}} )+\pi n,n \in Z\\ x=- \frac{\pi}{6}+\pi n,n \in Z\end{lgathered}
tgx=
3
x=arctg(
3
)+πn,n∈Z
x=
3
π
+πn,n∈Z
tgx=−
3
1
x=arctg(−
3
1
)+πn,n∈Z
x=−
6
π
+πn,n∈Z