Признак делимости чисел на 2 На 2 делятся все четные натуральные числа, например: 172, 94,67 838, 1670. Признак делимости чисел на 3 На 3 делятся все натуральные числа, сумма цифр которых кратна 3. Например: 39 (3 + 9 = 12; 12 : 3 = 4); 16 734 (1 + 6 + 7 + 3 + 4 = 21; 21:3 = 7). Признак делимости чисел на 4 На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4. Например: 124 (24 : 4 = 6); 103 456 (56 : 4 = 14). Признак делимости чисел на 5 На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0. Например: 125; 10 720. Признак делимости чисел на 6 На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно (все четные числа, которые делятся на 3). Например: 126 (б — четное, 1 + 2 + 6 = 9, 9 : 3 = 3). Признак делимости чисел на 9 На 9 делятся те натуральные числа, сумма цифр которых кратна 9. Например: 1179 (1 + 1 + 7 + 9 = 18, 18 : 9 = 2). Признак делимости чисел на 10 На 10 делятся все натуральные числа, оканчивающиеся на 0. Например: 30; 980; 1 200; 1 570. Признак делимости чисел на 11 На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11. Например: 105787 (1 + 5 + 8 = 14 и 0 + 7 + 7 = 14); 9 163 627 (9 + 6 + б + 7 = 28 и 1 + 3 + 2 = 6); 28 — 6 = 22; 22 : 11 = 2).
1) Предположим, что х - производительность пробоины, через которую вода поступает в лодку. Пусть у - производительность каждого из двух насосов.
Тогда 5х - уровень воды, который поднялся бы в лодке, если бы не работал насос. 5у - уровень воды, который должен был снизиться за 5 минут при работе одного насоса. Уравнение, описывающее ситуацию при работе одного насоса: 5х-5у = 20
3х - уровень воды, который поднялся бы в лодке за 3 минуты, если бы не работали насосы. 2у - производительность двух одинаковых насосов, работающих одновременно. 3•2у - уровень воды, который должен был снизиться за 3 минуты при работе двух одинаковых насосов. асоса. Уравнение, описывающее ситуацию при работе двух насосов: 3х-2•3у = 20-10
График прямой задается формулой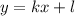 , где
, где 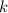 и
и 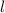 — некоторые коэффициенты,
— некоторые коэффициенты,  — независимая переменная, которая называется линейной функцией.
— независимая переменная, которая называется линейной функцией.
Имеем три точки: , где
, где 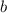 — параметр, который нужно найти.
— параметр, который нужно найти.
Подставляя соответствующие координаты в функцию, получаем систему из трех линейных уравнений с тремя неизвестными:
Из третьего уравнения: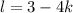 . Подставим
. Подставим 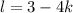 в первое и во второе уравнение:
в первое и во второе уравнение:
Выразим из второго уравнения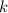 :
:
Подставим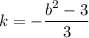 в первое уравнение:
в первое уравнение:
Решим полученное квадратное уравнение через дискриминант:
Таким образом, имеем: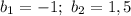
ответ: