42)
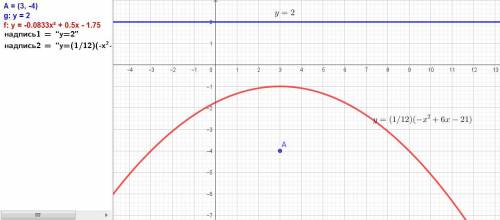
Дано: точка A(3;− 4) и прямая y = 2. Необходимо составить уравнение геометрического места точек, равноудаленных от заданной точки.
Пусть точка, соответствующая заданным требованиям, М(х; у).
Расстояние АМ² = (х - 3)² + (у - (-4))² = (х - 3)² + (у + 4)².
Так как по заданию расстояние АМ равно (2 - у), то подставим это значение в уравнение.
(2 - у)² = (х - 3)² + (у + 4)². Раскроем скобки.
4 - 4у + у² = х² - 6х + 9 + у² + 8у + 16. Приводим подобные.
12 у = -х² + 6х - 21.
ответ: у = (-1/12)х² + (1/2)х - (21/12). Это уравнение параболы.
x = 22, y = 18, z = 35
Пошаговое объяснение:
Нехай перше число х, друге у, третє z
Тоді x + y + z = 75
x = y + 4
z = x + 13 = (y + 4) + 13 = y + 17
(y + 4) + y + (y + 17) = 3y + 21
3y + 21 = 75
3y =54
y = 18
x = 18 + 4 = 22
z = 18 + 17 = 35