Пошаговое объяснение:
1. S = п*R^2
S = 3,14 * 2^2 =4п= 3,14 * 4 = 12,56 (cм^2)
2.S сектора=(п*R^2 *на угол)/360° ;
S=(п*6^2*60)/360=6п=6*3,14=18,84 (cм^2)
3.C=2πr
S=πr²=4π⇒r==2 (см
)
C=2*2π=4π=12,56 (см)
4.C=2πr=πd;
С=3,14*2=6,28 (см)
5.Длина дуги окружности: πr*n/180, где n - градусная мера дуги.
π*15*60/180=5π =5*3,14=15,7 (см)
6.длина дуги=альфа*r;
2п=альфа*12
альфа=2п:12=п:6=30 градусов
7.Диагональ квадрата больше его стороны в √2 раз. Значит, длина стороны квадрата равна 2. Диаметр вписанной в квадрат окружности равен его стороне, то есть d=2. По формуле длины окружности, l=2πr=πd ⇒ l=2π=2*3,14=6,28 (см)
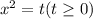 , тогда придем к уравнению вида
, тогда придем к уравнению вида 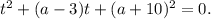 Поскольку t - положительное число, то корни квадратного трехчлена
Поскольку t - положительное число, то корни квадратного трехчлена 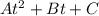 с действительными коэффициентами оба действительны и оба больше данного числа
с действительными коэффициентами оба действительны и оба больше данного числа 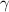 (
(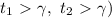 , когда
, когда 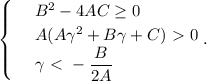
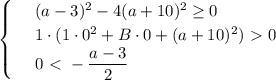
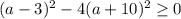 . Применяя формулу сокращенного умножения
. Применяя формулу сокращенного умножения 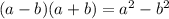 в левой части неравенства, получим
в левой части неравенства, получим 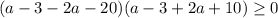 , тогда
, тогда 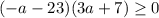 . Приравняв к нулю, получим корни
. Приравняв к нулю, получим корни 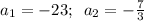
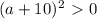 . Левая часть неравенства принимает только положительные значения, значит неравенство выполняется при
. Левая часть неравенства принимает только положительные значения, значит неравенство выполняется при 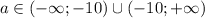
 . Умножив обе части неравенства на 2, получим
. Умножив обе части неравенства на 2, получим 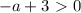 откуда
откуда 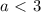
![a \in [-23;-10)\cup(-10;- \frac{7}{3} ]](/tpl/images/0775/5491/f18fe.png)
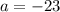 , то неравенство примет вид
, то неравенство примет вид 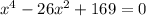 . Используя формулу сокращенного умножения
. Используя формулу сокращенного умножения 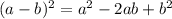 , получим
, получим 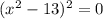 , тогда
, тогда 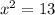 откуда
откуда 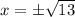 . Значит при а=-23 уравнение имеет 2 корня, следовательно, а=-23 нам не подходит.
. Значит при а=-23 уравнение имеет 2 корня, следовательно, а=-23 нам не подходит.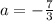 , то уравнение примет вид
, то уравнение примет вид 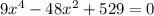 . Решив квадратное уравнение относительно
. Решив квадратное уравнение относительно 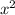 , имеем
, имеем 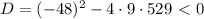 . Поскольку D<0, то квадратное уравнение действительных корней не имеет.
. Поскольку D<0, то квадратное уравнение действительных корней не имеет. 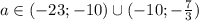
Пошаговое объяснение:
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Пример: Найти размах чисел 2, 5, 8, 12, 33.
Решение: Наибольшее число здесь 33, наименьшее 2. Значит, размах составляет 31:
33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Пример: Найти моду ряда чисел 1, 7, 3, 8, 7, 12, 22, 7, 11, 22, 8.
Решение: Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медиана.
В упорядоченном ряде чисел:
Медиана нечетного количества чисел – это число, записанное посередине.
Пример: В ряде чисел 2, 5, 9, 15, 21 медианой является число 9, находящееся посередине.
Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Пример: Найти медиану чисел 4, 5, 7, 11, 13, 19.
Решение: Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел:
(7 + 11) : 2 = 9.
Число 9 и является медианой данного ряда чисел.
В неупорядоченном ряде чисел:
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Пример 1: Найдем медиану произвольного ряда чисел 5, 1, 3, 25, 19, 17, 21.
Решение: Располагаем числа в порядке возрастания:
1, 3, 5, 17, 19, 21, 25.
Посередине оказывается число 17. Оно и является медианой данного ряда чисел.
Пример 2: Добавим к нашему произвольному ряду чисел еще одно число, чтобы ряд стал четным, и найдем медиану:
5, 1, 3, 25, 19, 17, 21, 19.
Решение: Снова выстраиваем упорядоченный ряд:
1, 3, 5, 17, 19, 19, 21, 25.
Посередине оказались числа 17 и 19. Находим их среднее значение:
(17 + 19) : 2 = 18.
Число 18 и является медианой данного ряда чисел.