Дано:
S=723 км.
t=13 ч.
t1=9 ч.
V1=55 км/ч.
V2=?
_________
Решение:
Мы знаем основную формулу пути:
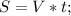 (Где V - скорость (км/ч - в нашем случае), t - время в пути).
(Где V - скорость (км/ч - в нашем случае), t - время в пути).
Разберем по участкам:
Первый участок пути автомобиль ехал со скоростью 55 км/ч, ехал он 9 часов. Можем найти путь, который он за данное время.
S1=55*9=495 км. - На первом участке пути.
Теперь найдем путь, который проехал автомобиль на втором участке пути:
S2=S-S1=723-495=228 км.
И время, которое затратил автомобиль на второй участок пути:
t2=t-t1=13-9=4 часа.
Теперь зная формулу пути, и выражая из нее скорость не трудно найти саму скорость на втором участке пути:
S=V*t-----> V=S/t;
Считаем:
V2=S2/t2=228/4=57 км/ч.
ответ: V2=57 км/ч.
ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
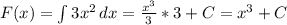
Подставляем в первообразную границы интегрирования:

2.
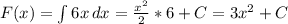
Подставляем в первообразную границы интегрирования:
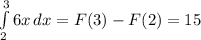
3.

Подставляем в первообразную границы интегрирования:
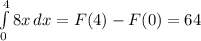
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
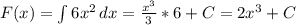
Подставляем в первообразную границы интегрирования:
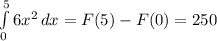
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

Время плавания (против теч. реки) - 1,7 ч
Время плавания (по теч. реки) - 2,6 ч
Скорость течения - 2,1 км/ч
Скорость катера - 28,2 км/ч
На сколько расстояние по теч. больше, чем против теч. - ?
1) 2,6 ч * (28,2 км/ч + 2,1 км/ч) = 78,78 км - S (расстояние по теч.)
2) 1,7 ч * (28,2 км/ч - 2,1 км/ч) = 44,37 км - S (расстояние против теч.)
3) 78,78 км - 44,37 км = 34,41 км - больше расстояние по теч, чем против
ответ: на 34,41 км