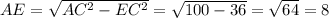 (см)
(см)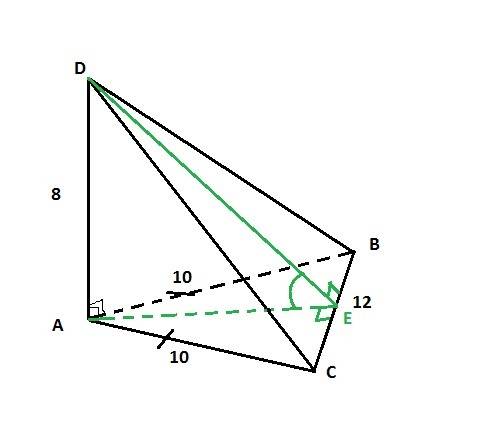
Перепишем первое неравенство системы:
a^2+7ax+8a-8x^2+28x+16
-8x^2+7x(a+4)+16+a^2+8a
Разложим квадратный трехчлен на множители.
D = 49*(a+4)^2+8*4*(16+a^2+8a)
D= 81*(a+4)^2, √D = 9*(a+4)
x1 = (-7(a+4)+9*(a+4))/(-2*8) = -1/8 *(a+4)
x2 = (-7(a+4)-9*(a+4))/(-2*8) = 4+a
Значит систему можно переписать в виде
(x-a-4)*(x+1/8 *(a+4)) ≤0
a ≤ x^2-4x
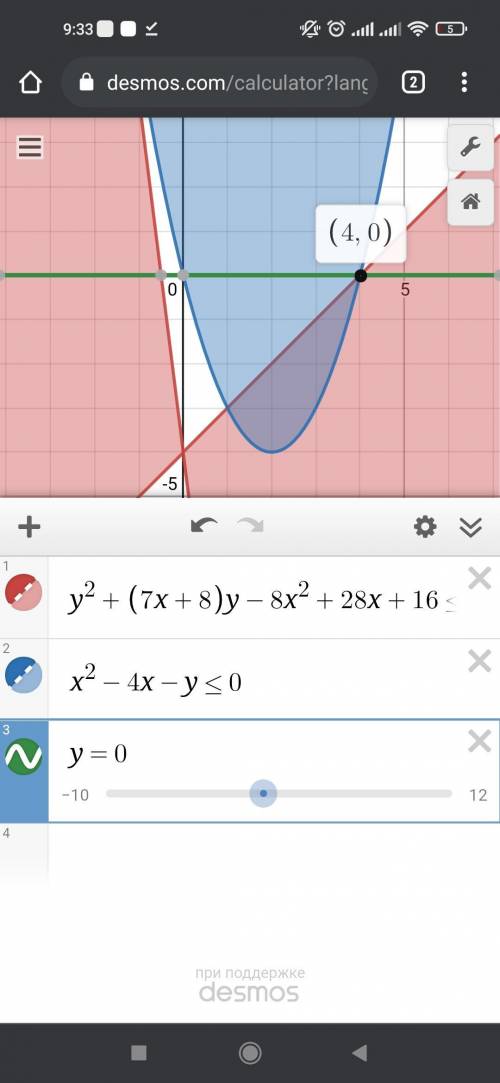
Рассмотрим координатную плоскость хОа (для нахождения единственного решения будем использовать прямую а, параллельную оси Х). Смотря на графики и систему неравенств, нам нужно пересечение того, что внутри параболы и внутри "углов"
Тогда(с.м. прикрепленный график) единственное решение при а=-4, а=0, а=12
Пошаговое объяснение:


Пошаговое объяснение:
1. х+2,7=3
х=3-2,7 (при переходе знак меняется на противоположный)
х=0,3
2. 3х-1=2(х-2)
3х-1=2х-4
3х-2х=-4+1
х=-3
3. 25-4х=12-5х
5х-4х=12-25 (когда 25 переносится, знак меняется на противоположный)
х=-13
4. 2х+7=х+5,5
2х-х=5,5-7
х=-1,5