количество угля х
на первой машине x т
на второй машине x т
на третьей машине х + 1,5 т
решение:
х+х+х+1,5=15
3х+1,5=15
3х=15-1,5
3х=13,5
х=13,5:3
х= 4,5 тугля привезли на второй машине.
Дано уравнение 7х²(3х+2)-(27х³+8)=0.
Раскроем скобки и приведём подобные.
21х³ + 14х² - 27х³ - 8 = 0.
Получаем кубическое уравнение:
-6х³ + 14х² - 8 = 0 или, сократив на -2:
3х³ - 7х² + 4 = 0. Первый корень виден сразу: это х1 = 1.
Разделим уравнение на (х - 1):
3х³ - 7х² + 4 | x - 1
3х³ - 3х² 3х² - 4x - 4
-4х² + 4
-4х² + 4x
-4x + 4
-4x + 4
0
Полученный трёхчлен разложим на множители как квадратное уравнение: 3х² - 4x - 4 = 0.
Д = 16 + 4*3*4 = 16 + 48 = 64.
х2 = (4 - 8)/(2*3) = -4/6 = -2/3.
х3 = (4 + 8)/(2*3) = 12/6 = 2.
ответ: х1 = 1, х2 = (-2/3 ), х3 = 2.
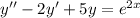
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является 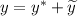 .
.
1) 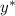 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
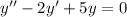
Применим метод Эйлера: сделаем замену 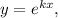 где
где 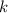 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 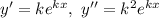
Получили характеристическое уравнение:
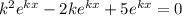
Разделим обе части уравнения на 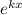 :
:
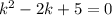
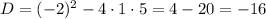
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
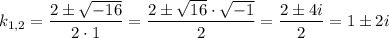
Тогда 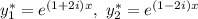
Воспользуемся формулой Эйлера: 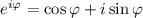
Фундаментальная система решений: 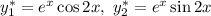 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 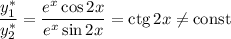
Общее решение: 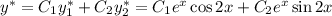
2) 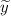 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 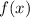 .
.
Здесь 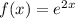 , причем
, причем 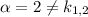 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 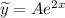 , где
, где 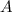 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда 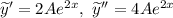 и
и 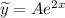 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 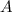 :
:
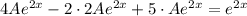
Разделим обе части уравнения на 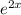
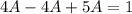
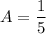
Таким образом, частное решение: 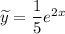
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
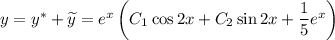
ответ: 
Пусть х тонн угля привезли на первой машине. На первой и второй машинах, по условию, привезли одинаковое количество угля, значит х тонн угля привезли и на второй машине. На третей машине привезли (х + 1,5) тонн угля. Всего привезли 15 тонн. Составим уравнение:
х + х + х + 1,5 = 15
3х = 15-1,5
3х = 13,5
х = 4,5
ответ: 4,5 тонны угля привезли на второй машине