Если мы рассматриваем плоскость, то все просто.
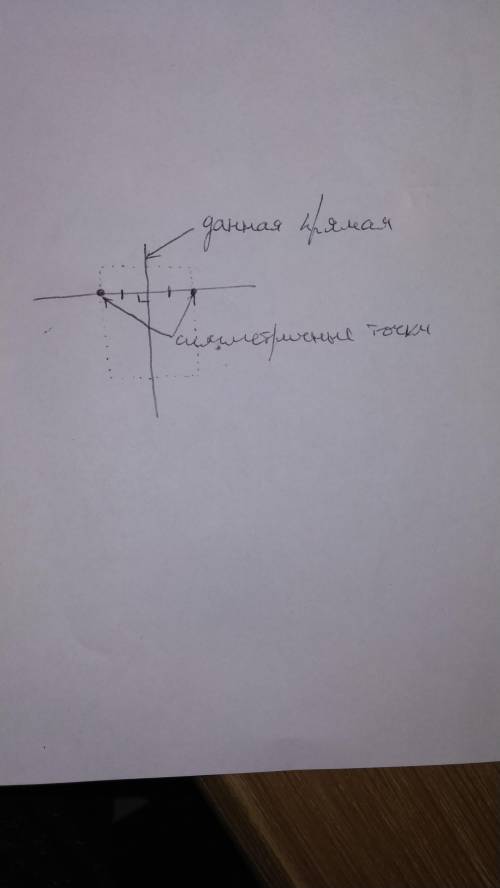
1) Выбираем точку фигуры.
2) Проводим через это прямую перпендикулярную данной
3) Откладываем от данной прямой на продолжении начерченной отрезок равный по длине расстоянию от нашей точки, до данной прямой.
4) Сравниваем. Если конец отрезка попал на другую точку фигуры, то эти точки симметричны относительно данной прямой.
5) Если так проделать с каждой точкой фигуры (так чтобы точке с одной стороны соответствовала точка, и при том только одна, с другой) то мы получим симметричную фигуру относительно данной прямой
Из точки М проведен перпендикуляр МD, равный 6 см., к плоскости квадрата АВСD. Наклонная МВ образует с плоскостью квадрата угол 60°. Доказать, что треугольники МАВ и МСВ прямоугольные. Найдите сторону квадрата. Докажите, что треугольник АВD является проекцией треугольника МАВ на плоскость квадрата, и найдите его площадь.
рисунок к задаче 196 Угол между прямой и плоскостью - это угол между этой прямой и её проекцией на эту плоскость. Т.е. ∠МВD=60°.
Рассмотрим наклонную МС, проекцию CD и прямую в ВС. Угол ВСD прямой (угол квадрата). По теореме о трех перпендикулярах угол МСВ тоже равен 90 градусов. А треугольник МСВ прямоугольный. Аналогично треугольник МАВ тоже является прямоугольным.
MD перпендикулярна плоскости квадрата, а значит перпендикулярна и любой прямой (BD к примеру) в этой плоскости. Рассмотрим прямоугольный треугольник МВD. В нем:
BD=MD * ctg60°
BD=6 * (корень из 3)/3 BD=2 корня из 3
Известно, что диагональ квадтрата больше его стороны в корень из 2 раз, поэтому:
АВ=BD/(корень из 2)
АВ=(2 корня из 3)/(корень из 2)=корень из 6
Две вершины треугольника АМВ уже лежат в плоскости АВСD, а точка М ортогонально спроектировна в точку D. Поэтому треугольник АBD является проекцией треугольника АМВ. SABD=1/2 * АВ2=3
Пошаговое объяснение: