Здравствуйте мне нужна с примерами с развернутым ответом (И сделайте это всерьез) заранее Найдите значение выражения
-90 + 7,0 * (-10
2) Выражения
0,6 * (-10 + 50

👇

Увидеть ответ

Ответ:

kogoch

17.05.2020

1) -7090 2) -550

Пошаговое объяснение:

-90 + 7 * (-10)^3 --> -10^3 = -10 * (-10) *(-10) = -1000 минус сохраняется, потому что знак степени нечётный

-90 + 7 * (-1000) --> Умножаем -1000 на 7, будет -7000

-90 - 7000 --> если два минуса, то добавляем числа и оставляем минус

-7090

0,6 * (-10)^3 + 50 --> --> -10^3 = -10 * (-10) *(-10) = -1000 минус сохраняется, потому что знак степени нечётный

0,6 * (-1000) + 50 --> 0,6 * (-1000) нечётное кол-во минусов, знак минус. Переносим кому на 3: раз: 6, два: 60, три: 600

-600 + 50 = -550

4,7(4 оценок)

Открыть все ответы

Ответ:

Aleksandra00123

17.05.2020

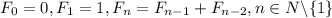
$F_0=0,F_1=1, F_n=F_{n-1}+F_{n-2}, n\in N\backslash\{1\}$

Заметим, что 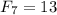F_7=13

Докажем, что, начиная с 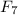F_7 , последовательность Фибоначчи периодическая по модулю 1000.

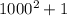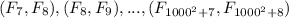Рассмотрим 1000^2+1 пару чисел $(F_7,F_8),(F_8,F_9),...,(F_{1000^2+7},F_{1000^2+8})$ .

Каждое из чисел каждой из пар дает один из 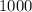1000 остатков по модулю 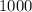1000 . Тогда всего вариантов пар остатков от деления на 1000 может быть 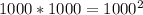1000*1000=1000^2 (1000 вариантов остатков 1ого числа пары и 1000 вариантов у 2ого).

Тогда, по принципу Дирихле, в рассматриваемом мн-ве пар найдутся хотя бы 2 пары чисел, соответствующие элементы которых сравнимы по модулю 1000 - а, с учетом определения последовательности Фибоначчи, это и означает периодичность остатков ее членов по модулю 1000.

Возьмем 2 такие пары с наименьшими номерами. Пусть это пары 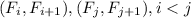$(F_i,F_{i+1}), (F_j,F_{j+1}), i$ . Покажем, что i=7 .

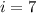Пусть не так, и .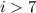

По построению, 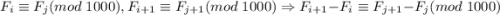$F_i\equiv F_j(mod \;1000),F_{i+1}\equiv F_{j+1}(mod \;1000)\Rightarrow F_{i+1}-F_{i}\equiv F_{j+1}-F_{j}(mod \;1000)$

Но, по определению последовательности Фибоначчи, 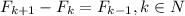$F_{k+1}-F_{k}=F_{k-1},k\in N$ . А значит 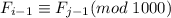$F_{i-1}\equiv F_{j-1}(mod\; 1000)$ . А тогда соответствующие элементы пар чисел 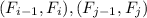$(F_{i-1},F_i),(F_{j-1},F_j)$ сравнимы по модулю 1000 - противоречие с тем, что 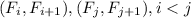$(F_i,F_{i+1}), (F_j,F_{j+1}), i$ - пары с наименьшими номерами.

Значит 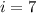i=7 .

А это означает, что в последовательности остатков от деления членов последовательности Фибоначчи на 1000 найдется сколь угодно чисел, сравнимых с 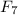F_7 по модулю 1000. Т.к последовательность возрастающая и неограниченная, начиная со 2ого члена, это утверждение эквивалентно условию задачи.

Доказано.

________________________________

Можно доказать аналогичным образом и более общее утверждение: последовательность чисел Фибоначчи по модулю 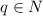$q\in N$ периодическая (вышеприведенные рассуждения - частный случай этого док-ва). Длина периода такой последовательности обозначается 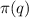$\pi(q)$ и называется период Пизано.

4,5(7 оценок)

Ответ:

саша4290

17.05.2020

Чувство собственного достоинства_ это моральная добродетель, состоящая в том, что личное достоинство человека доросло в нем до самоосознания. Когда человек чувствует что закон может определять лишь его совместной жизни с другими, но не цели его жизни и не то, во что ему надлежит верить- это он чувствует собственное личное достоинство.
-философская категория, обозначая некий элемент бытия, объект или фрагмент.
-универсальная культура субъектного ряда, фиксирующая возможность деятельности и поведения в усло как право

4,6(95 оценок)

Это интересно:

Образование-и-коммуникации

12.02.2023

Как написать детское стихотворение...

Здоровье

26.01.2020

Как правильно составить аптечку для детей: полезные советы и рекомендации...

Хобби-и-рукоделие

25.01.2022

Как подшить штаны: пошаговая инструкция...

Компьютеры-и-электроника