![\beta\in[0;1]:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{n}}=\alpha](/tpl/images/1121/0389/0e53a.png)
Тогда, по признаку Коши, при 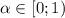 ряд сходится, при
ряд сходится, при 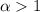 расходится.
расходится.
При 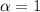 имеем
имеем 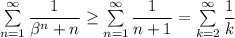 Гармонический ряд расходится, а тогда исходный ряд расходится по признаку сравнения.
Гармонический ряд расходится, а тогда исходный ряд расходится по признаку сравнения.
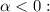
При 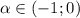 ряд сходится, т.к. ряд из модулей (по доказанному выше) сходится.
ряд сходится, т.к. ряд из модулей (по доказанному выше) сходится.
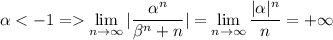 необходимое условие не выполнено, а значит ряд расходится.
необходимое условие не выполнено, а значит ряд расходится.
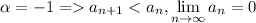 , а тогда по признаку Лейбница ряд сходится.
, а тогда по признаку Лейбница ряд сходится.
![\beta1:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n}}=\dfrac{\alpha}{\beta}](/tpl/images/1121/0389/8e2ed.png)
Тогда при 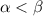 ряд сходится, при
ряд сходится, при 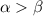 расходится.
расходится.
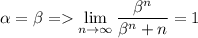 - необходимое условие не выполнено, ряд расходится.
- необходимое условие не выполнено, ряд расходится.
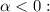
Тогда при 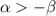 ряд сходится.
ряд сходится.
При 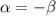 необходимое условие не выполнено, ряд расходится.
необходимое условие не выполнено, ряд расходится.
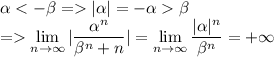 необходимое условие не выполнено, ряд расходится.
необходимое условие не выполнено, ряд расходится.
По итогу ряд сходится только на ![[-1;1)\times[0;1] \;\;\bigcup\;\; (-\beta;\beta)\times[\beta;+\infty),\forall\beta1](/tpl/images/1121/0389/77aa2.png)
- Здравствуйте Ольга Леонидовна( Имя учителя! :))
- Как ты отдыхал этим летом? Все ли книги прочла? Рада ли 1 сентября! Первому Звонку?
- Отдыхала просто замечательно! На даче почьти всё лето! О 1 сентября ну как сказать! Немного.
- Ну хорошо, садитесь по местам мы начнём 1 урок в этом учебном году!
- Сәлам
- Исәнмесез Ольга Леонидовна( Исемен укытучылар! :))
- Син ничек ял иткђн, бу җәйдә? Барысы да бармы китаплар прочла? Шат бармы 1 сентябрь! Беренче Шалтырату?
- Отдыхала искиткеч яхшы! Дачада почьти җәй буе! О, 1 сентябрь ничек инде әйтергә! Бераз.
- Ярар, яхшы, садитесь урыннар буенча башлаячакбыз 1 дәрес уку елында!