.(Знайка начертил 3 разных по длине и цвету отрезка. соблюдая такие условия. длина каждого отрезка целое число (см) красный длиннее 13 см но короче 16 см, синий длиннее 14 см, но короче 17 см, зелёный длиннее 13 см, но короче 15 см.
начертить такие отрезки. как изменяется выполнение ,если у некоторых отрезков она окажется одинаковой длинной, начертить возможные решения.).

👇

Увидеть ответ

Ответ:

Волвлчлчлч

13.11.2020

1) Красный сначала можно начертить длиной 15см

2) Синий можно начертить 16см(при красном отрезке длиной 15см)

3) Зелёный можно начертить 14см

Это единственное решение, так как по условию все отрезки разной длины, а если мы начертим одинаковой, то нужно изменить условие.

Если чертить одинаковые то есть ещё варианты решения:

1) красный 14см

2)синий 15см

3)зелёный 14см

Ещё вариант:

1)красный 15см

2)синий 15см

3)зелёный 14см

Ещё:

1)красный 14см

2)синий 16см

3)зелёный 14см

Наверное это всё

4,4(74 оценок)

Открыть все ответы

Ответ:

Крошка21155

13.11.2020

Пошаговое объяснение:

1)уравнение плоскости Q, проходящей через точки

А (–6; –4; 2);

В (5; –2; –1);

С (5; 6; –4);

для составления уравнения плоскости используем формулу

$\left[\begin{array}{ccc}x-z_A&y-y_A&z-z_A\\x_B-x_A&y_B-y_A&z_B-z_A\\x_C-x_A&y_C-y_A&z_C-z_A\end{array}\right] =0$

$\left[\begin{array}{ccc}x-(-6)&y-(-4)&z-2\\5-(-5)&(-2)-(-4)&-1-2\\5-(-6)&6-(-4)&-4-2\end{array}\right] =0$

(x -(-6))(2*(-6) - (-3)*10) - (y -(-4))(11*(-6) -(-3)*11 ) + (z -2)(11*10 -2*11) = 0

18(x -(-6)) + 33(y - (-4)) + 88(z - 2) = 0

и вот мы получаем уравнение плоскости Q

Q : 18x + 33y + 88z +64 = 0

2) канонические уравнения прямой АВ. А(–6; –4; 2); В(5; –2; –1);

формула канонического уравнения прямой

$\frac{x-x_A}{x_B-x_A} =\frac{y-y_A}{y_B-y_A} =\frac{z-z_A}{z_B-z_A}$

наша формула прямой

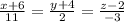
$\frac{x+6}{11} =\frac{y+4}{2} =\frac{z-2}{-3}$

3) уравнение плоскости G, проходящей через точку D(2; 8; 6) перпендикулярно прямой АВ

будем искать прямую в виде A(x-x_D)+B(y-y_D)+C(z-z_D)=0

здесь А, В, С - координаты направляющего вектора.

поскольку G ⊥ АВ, то нормаль АВ будет направляющим вектором для G ⇒ s = n = (11, 2, -3)

и вот формула

G : 11y + 2y - 3z -20 =0

4) расстояние от точки D(2; 8; 6) до плоскости Q : 18x + 33y + 88z +64=0

для расчета нам потребуется

А = 18; В = 33; С = 88; D = 64;

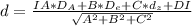
$d=\frac{IA*D_A+B*D_e+C*d_z+DI}{\sqrt{A^2+B^2+C^2} }$

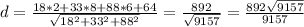
$d=\frac{18*2+33*8+88*6+64}{\sqrt{18^2+33^2+88^2} } =\frac{892}{\sqrt{9157} } =\frac{892\sqrt{9157} }{9157}$

4,6(67 оценок)

Ответ:

Vania54

13.11.2020

Пошаговое объяснение:1. 10/20 * 6/19 * 4/18 - это целевая вероятность при одном сценарии (когда берётся наугад сначала изделие 1 сорта, потом 2, потом 3). Поскольку таких сценариев (3! = 6), а произведение везде будет одинаковое, то имеем ответ: 6 * (1/2 * 6/19 * 2/9)

2. Найти вероятность того, что обе детали бракованные.

Во-первых, надо допустить, что деталей бесконечное множество. То есть после взятия одной детали соотношение остаётся 40% к 60%. Если мы такое допустили, то можно приступить к расчёту.

Сумма вероятностей четырёх сценариев:

1. взяли две бракованных первого завода

2. взяли две бракованных второго завода

3. взяли бракованную первого завода и потом бракованную второго завода

4. взяли бракованную второго завода и потом бракованную первого завода

для 3 и 4 вероятность одинаковая.

ответ: 0.4 * 0.04 * 0.4 * 0.04 + 0.6 * 0.02 * 0.6 * 0.02 + 2 * (0.4 * 0.04 * 0.6 * 0.02)

Найти вероятность того, что обе детали бракованные изготовлены первым заводом.

Это у нас Сценарий 1.

ответ: 0.4 * 0.04 * 0.4 * 0.04

4,8(52 оценок)

Это интересно: