Это показательное уравнение вида , где неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения представить в виде числа со степенью так, чтобы в основании было число . Это явно число (проверка: ).
Значит теперь, когда наше показательное уравнение имеет вид , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. .
Из этого следует, что ответ нашего показательного уравнения равен .
Евра́зия (англ. Eurasia) - самый большой материк Земли, состоящий из двух частей света - Европы и Азии. Более 1/3 части суши планеты приходится на Евразию; её площадь, вместе с прилегающими островами, около 53,4 млн. км2, из них на острова приходится около 2,75 млн. км2. При этом 4/5 из них приходится на Азию и 1/5 часть — на Европу — две части света, которые традиционно выделяют в составе Евразии. Названия этих частей света произошли в глубокой древности и означают в переводе с языка ассирийцев: «эреб» — «запад, закат» и «асу» — «восток, восход» (Солнца). Сухопутная граница между Европой и Азией несколько раз пересматривалась. В настоящее время её принято проводить вдоль восточного подножия Уральских гор (примерно по 60° в. д.), реке Эмбе, северному побережью Каспийского моря, Кумо-Манычской впадине, севернее Кавказа, на Таманский полуостров. Далее граница идёт по Чёрному морю и проливам, соединяющим Чёрное море со Средиземным.
Это показательное уравнение вида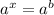
, где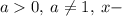 
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения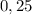
представить в виде числа со степенью так, чтобы в основании было число 
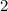. Это явно число 
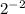(проверка: 
).
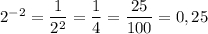Значит теперь, когда наше показательное уравнение имеет вид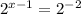
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение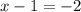
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 
.
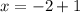Из этого следует, что ответ нашего показательного уравнения равен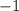
.
ответ: