ДУМАЕМ
Мысль 1. Решение надо не только вычислить, но ещё и изобразить на координатном луче.
Мысль 2. Что выбрать за единичный отрезок на этом координатном луче. Если взять за него - с = 1 клетка в тетради. Пробуем.
РЕШЕНИЕ
Рисунок к задаче в приложении.
На координатном луче с единичным отрезком в 1 клетку отметили цифры 25 и 30. Теперь делим его на 20 частей и
(30 - 25):20 = 5/20 = 1/4 клетки это мелкие деления. Как же изобразить задание - так мелко, что и цифры написать негде.
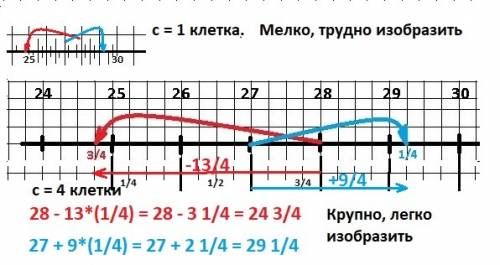
Мысль 3. Получилось плохо. Надо увеличить единичный отрезок - как раз в четыре раза. Получилось что от 25 до 30 - как раз (30-25)*4 =20 клеток, а каждая клетка будет равна 1/4. Делаем другой рисунок. Мысль 4. Если направо - больше и надо прибавить, то налево - меньше и надо вычесть.
РАСЧЕТ на рисунке в приложении.
Докажем по индукции, что после каждого нечетного переливания в первом сосуде будет половина всей воды, т.е. 5 литров.
После первого переливания, это так.
Пусть после очередного нечетного переливания у нас в первом сосуде оказалось 5 л. и во втором, соответственно, тоже 5 л. Тогда следующим переливанием (оно имеет четный номер) мы какую-то часть (пусть 1/k -ую) переливаем из второго сосуда в первый, т.е. в первом станет 5+5/k=5(1+1/k). Значит следующим (нечетным) переливанием мы во второй сосуд выливаем из первого 1/(k+1) часть, т.е. в первом останется
5(1+1/k)-5(1+1/k)/(k+1)=5(1+1/k)(1-1/(k+1))=5*(k+1)/k *k/(k+1)=5.
Таким образом, каждые 2 переливания начиная с 1-го оставляют в каждом сосуде по 5 литров. Значит и после 2017-го переливания, т.к. оно имеет нечетный номер, в первом сосуде будет 5 литров.