 , лежит на перпендикуляре, проведённым из точки А к этой прямой.
, лежит на перпендикуляре, проведённым из точки А к этой прямой. можно провести в плоскости, перпендикулярной прямой
можно провести в плоскости, перпендикулярной прямой  .
. будет нормальным вектором плоскости и точка А лежит в этой плоскости.
будет нормальным вектором плоскости и точка А лежит в этой плоскости.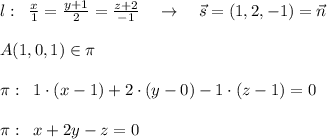
 и плоскости
и плоскости 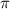 .
. 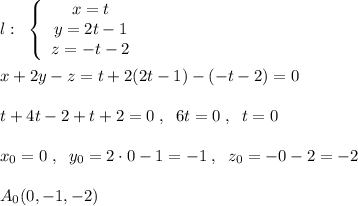
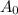 является серединой отрезка
является серединой отрезка 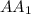 .
.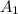 .
.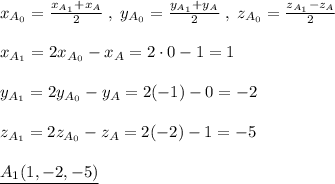
2,3x=46
x=46:2,3
x=20
1)20
2)0,6x=12
3)0,7x=14