Відповідь:
1. А) -12.
2. Г) -10, -8, 0, 7, 2.
3. Б) -13+4=-9.
4. Г) -2•12=-24.
5. |х|=9
х=9 або х=-9.
13х-5=5х+11
13х-5х=11+5
8х=16
х=2.
6. 4b-11b=4-11=-7.
8-(х+8)=8-8х=х.
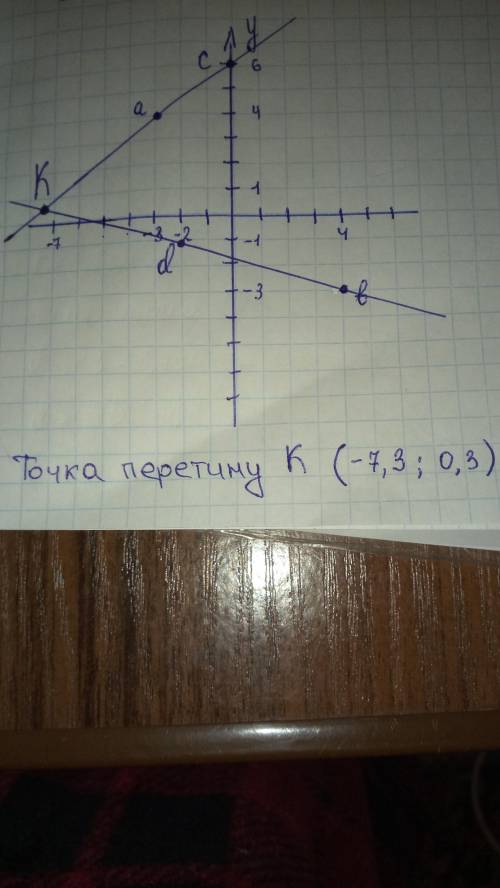
7. На фото знизу.
8. Восьме завдання у вас не зовсім зрозуміло, напишете в коментарях, я дам відповідь.
9. -2,7•(-0,2)+72+7,2•(-0,2)-8=0,54+72-1,44-8=63,1.
10. Нехай на другій полиці було х книжок. Тоді на першій полиці 5х книжок.
Складаємо рівняння:
х+12=5х-20
4х=32
х=8(кн.)– на другій полиці
Тоді, на першій полиці 5•8=40(кн.)
Відповідь: на першій полиці спочатку було 40 книг, а на другій 8 книг.
2.
В случае, если точки окружности А и С, данные в условии, ограничивают диаметр окружности, и точка В лежит на продолжении этого диаметра (рис.1):
АС = АВ - СВ = 50 - 20 = 30 (см)
Радиус окружности:
ОА = ОС = АС : 2 = 30 : 2 = 15 (см)
------------------------------------------
В случае, когда максимально удаленной точкой окружности от точки В является точка касательной к окружности:
ВА - касательная к окружности.
Тогда: ВА ⊥ ОА
В прямоугольном треугольнике ОАВ:
ОВ = R + CB = R + 20 (см) - гипотенуза
OA = R - катет
АВ = 50 см - второй катет
Тогда по т.Пифагора:
(20 + R)² = 50² + R²
400 + 40R + R² = 2500 + R²
40R = 2100
R = 52,5 (см)
-------------------------------------------
3.
Так как АВ и АС - касательные, то АВ = АС и АО - биссектриса ∠САВ. (по 2-му свойству касательных к окружности)
ΔОМС = ΔОМВ по двум сторонам и углу между ними
Тогда ВС ⊥ АО и ВМ = МС
В прямоугольном треугольнике ΔВМА:
∠ВАМ = 30° => ВМ = АВ : 2 = 5 : 2 = 2,5 (см)
Тогда:
ВС = 2·ВМ = 5 (см)
-------------------
Или так:
АО - биссектриса ∠САВ => ∠САВ = 60°
ΔОМС = ΔОМВ по двум сторонам и углу между ними
Тогда: СМ = МВ и ∠САВ - равнобедренный с углом при вершине ∠САВ = 60°
Следовательно, по теореме о сумме внутренних углов треугольника:
∠ВСА = ∠СВА = 60°
Тогда ΔСАВ - равносторонний и ВС = 5 см