![\int \frac{\sqrt{1+\sqrt{x}}}{x\sqrt[4]{x^3} } dx = \int ((1+x^{\frac{1}{2}})^\frac{1}{2}*x^{-\frac{7}{4}})dx = \int (x^{-\frac{7}{4}}*(x^{\frac{1}{2}}+1)^\frac{1}{2})dx; \\|m=-\frac{7}{4}\\| a = 1\\|n = \frac{1}{2}\\ |b = 1\\|p=\frac{1}{2}\\\frac{m+1}{n} + p = -1 \in Z = t^2 = 1 + x^{-\frac{1}{2}} = x^{-\frac{1}{2}} = t^2-1 = x^{-1} = (t^2-1)^2 = x = (t^2-1)^{-2} = dx = -2(t^2-1)^{-3}*2tdt = -4t(t^2-1)^{-3}dt\\](/tpl/images/1228/3430/755c5.png)
![\int \frac{\sqrt{1+\sqrt{x}}}{x\sqrt[4]{x^3} } dx = \int \frac{\sqrt{1+\sqrt{(t^2-1)^{-2}}}}{(t^2-1)^{-2*\frac{7}{4} }} * -4t(t^2-1)^{-3}dt = \int \frac{\sqrt{1 + \frac{1}{t^2-1}}}{(t^2-1)^{-\frac{7}{2} }} *-4t(t^2-1)^{-3}dt =](/tpl/images/1228/3430/0dfd0.png)
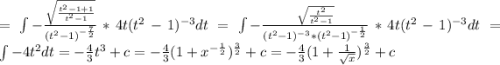
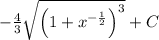
Пошаговое объяснение:


7 см
Пошаговое объяснение:
Если прямая перпендикулярна к плоскости, то она перпендикулярна к каждой прямой в этой плоскости, поэтому все треугольники AOK, BOK, COK и DOK с прямым углом.
К тому же они все одинаковы, так как имеют общий катет OK, диагонали квадрата также одинаковы и делятся в точке пересечения пополам OA=OB=OC=OD.
Значит, KA=KB=KC=KD, поэтому необходимо рассчитать только одно расстояние.
Проведём расчёты в треугольнике AOK. Если сторона квадрата равна 9 см, то диагональ квадрата равна 92√ см. AO равно половине диагонали.
По теореме Пифагора рассчитаем KA:
KA=(3)2+(92√2)2−−−−−−−−−−−−−−√≈ 7 см.