Вершини трикутника ABC мають координати A(10;−1), B(−2;−6), C(−6;−3) . Скласти рівняння сторін трикутника.

Question

Математика: Вершини трикутника ABC мають координати A(10;−1), B(−2;−6), C(−6;−3) . Скласти рівняння сторін трикутника.

тикон3 · Accepted Answer

Л е м м а: Пусть 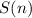S(n) -- сумма цифр числа 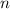. Тогда 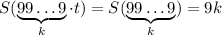$S(\underbrace{99\ldots9}_{k}\cdot t) = S(\underbrace{99\ldots9}_{k}) = 9k$ , если длина 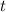не превосходит 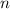. Иными словами сумма цифр числа, состоящего из девяток, не меняется при умножении на достаточно короткое число.

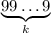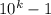Д о к а з а т е л ь с т в о достаточно механическое: просто записываем число $\underbrace{99\ldots9}_{k}$ как $10^{k}-1$ , а разность 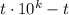$t\cdot10^{k} - t$ считаем в столбик, учитывая перенос единицы.

Теперь пусть дано число 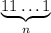$\underbrace{11\ldots1}_{n}$ . Возьмем число 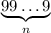$\underbrace{99\ldots9}_{n}$ , тогда его частное с первым числом равно 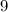. Умножим в таком случае 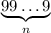$\underbrace{99\ldots9}_{n}$ на 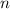. Длина числа 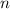меньше 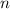для всех 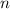, кроме (что представляет собой тривиальный случай), потому по лемме $\left[\underbrace{99\ldots9}_{n}\cdot n\right]\div \underbrace{11\ldots1}_{n} = 9n = S(\underbrace{99\ldots9}_{n}) = S(\underbrace{99\ldots9}_{n}\cdot n)$ .

MOGZ ответил