Пошаговое объяснение:
Уравнение первой прямой
2*у = - 3*х +6
у = - 1,5*х + 3 - прямая
k = - 3/2
Проводим перпендикулярную прямую из точки М.
У неё k = - 1/(-3/2) = 2/3
Дано: Точка M(2,-1), наклон k = 2/3
b = Mу - k*Mx = -1 - (2/3)*(2) = -2 1/3
Уравнение прямой - Y(M) = 2/3*x - 2 1/3
Находим точку пересечения прямых.
-3/2*x +3 = 2/3*x - 2 1/3
Аx = (-2 1/3 - 3)/(-3/2 - 2 1/3) = 5 1/3 : 2 1/6 = 2 6/13 ≈ 2,46
и Аy = - 9/13 ≈ - 0,69
И по теореме Пифагора.
C² = (2.46-2)² + (-0.69 - 1)² = 0.46² + 0.31² = 0.2116+0.0961 = 0.308
C = √0.308 = 0.55 - ответ.
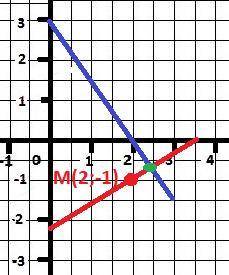
Рисунок к задаче в приложении.
Обозначим того, у кого больше всего друзей через A, а того, у кого их меньше всего – через B. В первом случае A дружит со всеми, а B – только с одним человеком, то есть только с A. Во втором случае B не дружит ни с кем, а A дружит со всеми, кроме одного, то есть со всеми, кроме B.
Итак, в каждом из случаев A дружит с Петей, а B – нет. Переведём A и B в другой класс. Как мы уже видели, A дружит со всеми из оставшихся, а B – ни с кем из оставшихся. Поэтому после перевода у каждого стало на одного друга меньше (среди одноклассников). Значит, у оставшихся Петиных одноклассников снова будет разное число друзей среди одноклассников.
Теперь снова переведём самого "дружелюбного" и самого "нелюдимого" в другой класс и т. д.
Повторяя эти рассуждения 14 раз, мы переведём в другой класс 14 пар школьников, в каждой из которых ровно один Петин друг. Итак, друзей у Пети 14
ответ:14