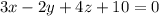
Пошаговое объяснение:
Общее уравнение плоскости: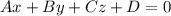 
, где 
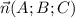-нормальный вектор плоскости(вектор, перпендикулярный этой плоскости)
Так как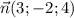 
, то уравнение плоскости примет вид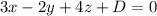 
Приведем полученное уравнение к уравнению плоскости в отрезках (деление на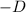 
возможно, так как 
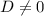- иначе отрезок на оси Оу был бы равен 0, плоскость проходила бы через начало координат):
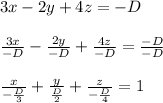
Получили уравнение плоскости в отрезках вида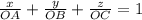 
, где ОА, ОВ, ОС - отрезки, отсекаемые плоскостью на осях Ох, Оу, Оz соотвественно
Так как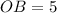 
, то 
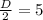и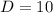 
Общее уравнение плоскости: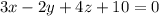
№ 1. № 2.
4 - 2х + 4х = 10 2 : х = 6 - 2
4х - 2х = 10 - 4 2 : х = 4
2х = 6 х = 2 : 4
х = 6 : 2 х = 0,5
х = 3
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
№ 3.
1/2 : 1/10 · 0,2 - 1/100 = 99/100 (или 0,99 в десятичных дробях)
1) 1/2 : 1/10 = 1/2 · 10/1 = 10/2 = 5
2) 5 · 0,2 = 1
3) 1 - 1/100 = 100/100 - 1/100 = 99/100 = 0,99