10+30=40км\скорость сближения:
200-80=120км
120:40=3-встретятся, значит правильное решение под В
Примем объем бака за 1. Тогда:
1/20 - скорость наполнения бака в минуту через первую трубу;
1/30 - скорость наполнения бака в минуту через вторую трубу.
Найдем совместную производительность труб:
\frac{1}{20} +\frac{1}{30} =\frac{30}{600} +\frac{20}{600} =\frac{50}{600} =\frac{1}{12}
20
1
+
30
1
=
600
30
+
600
20
=
600
50
=
12
1
Найдем за сколько минут бак наполнится через обе эти трубы:
1 : \frac{1}{12} =121:
12
1
=12
ответ: 12 минут.
Пошаговое объяснение:
это правильно можно корону чтобы я мог перити на следующий уровень
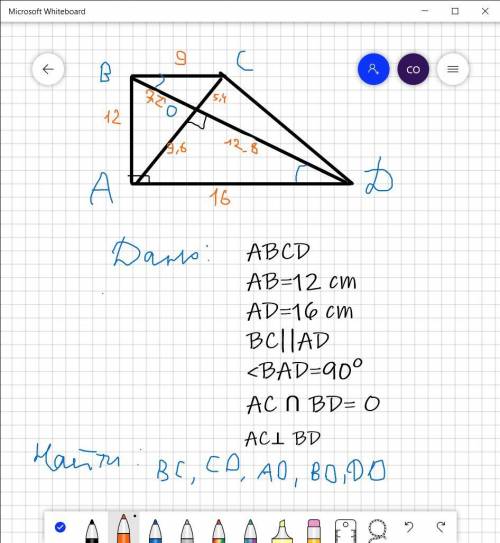
ответ: 9 см; 5,4 см; 9,6 см; 7,2 см; 12,8 см
Пошаговое объяснение:
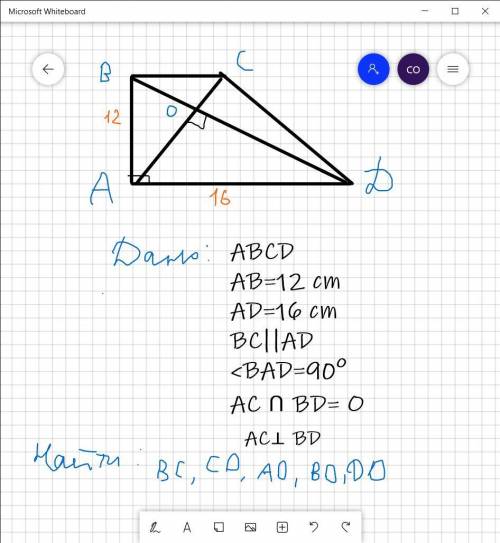
на фото рисунок и дано
Прежде всего мы можем узнать ВД из ΔАВД
Это египетский треугольник, т.к. угол ВАД=90° и катеты соотносятся как 3:4 (12:16=3:4)
k=12/3=4
Поэтому гипотенуза ВД=5k=5*4=20 см
У трегольников ΔАВО и ΔАДО общая сторона--АО. Причем оба прямоугольные, поэтому по теореме Пифагора выводим катет АО из обоих треугольников.
из ΔАВО АО²=АВ²-ОВ²
из ΔАДО АО²=АД²-ОД²
АВ²-ОВ²=АД²-ОД²
И для удобства обозначим ОВ=х, ОД=20-х
12²-х²=16²-(20-х)²
144-х²=256-400+40х-х²
144=256-400+40х
40х=144+400-256
40х=288
х=7,2 см
ОВ=7,2 см
ОД=20-х=20-7,2=12,8 см
Теперь подставляем результат в формулу
АО²=АВ²-ОВ²
АО²=144-(7,2)²=92,16
АО=9,6 см
Т.к. ВС параллельна АД, то ВД--сечная, поэтому их внутренние разносторонние углы СВД и ВДА равны. Также известно, что ВОС=АОД (как вертикальные), из этого делаем вывод, что треугольники ΔДОА ~ΔВОС подобны
Поэтому ВС/АД=ВО/ОД
ВС=АД*ВО/ОД=16*7,2/12,8= 9 см
И, наконец, ОС/АО=ВС/АД
ОС=ОА*ВС/АД=5,4 см
Фотку с обозначеными сторонами тоже оставила
Предположим, между А и В - 60 км. Из А едет велосипедист (10 км/ч),
из В - мотоциклист (40 км/ч).
Через час мотоциклист удалится на 40 км от В и не доедет 20 км до А,
а велосипедист, будет в 10 км от А и от мотоциклиста.
Ещё через час мотоциклист отъедет уже 80 км от В и уже 20 км - от А.
Велосипедист тоже уже отъедет 20 км от А в другую сторону.