Question

Задание №15 ЕГЭ математика
Реши неравенство

Answer 1

Из знаменателя нам нужно только взять ограничение подкоренного выражения, которое и будет являться областью определения неравенства (в числителе ограничений нет): $x+4\geq 0 \Rightarrow \boxed{x\geq -4}$

Помним про это.

Теперь решаем само неравенство

$\displaystyle 26^{|x|}=(2\cdot 13)^{|x|}=2^{|x|}\cdot 13^{|x|}$ - это нам потребуется

Заметим, что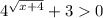 $\displatstyle 4^{\sqrt{x+4}}+3 0$ для любых $x$, поэтому умножим все неравенство на знаменатель и ничего не поменяется, избавимся от дроби. И сразу запишем в числителе то, что уже преобразовали.

$\displaystyle 2^{|x|}\cdot 13^{|x|}-2^{|x|}-2\cdot 13^{|x|}+2\geq 0 ;\ 13^{|x|}(2^{|x|}-2)-(2^{|x|}-2)\geq 0; \\ (2^{|x|}-2)(13^{|x|}-1)\geq 0$

Чтобы решить полученное неравенство методом интервалов, найдем нули выражения, стоящего левее знака:

$\displaystyle \\ (2^{|x|}-2)(13^{|x|}-1)= 0 \Leftrightarrow \left [ {{2^{|x|}-2=0} \atop {13^{|x|}-1=0} \right. \Rightarrow \left [ {{2^{|x|}=2^1} \atop {13^{|x|}}=13^0} \right. \Rightarrow \\ \left [ {{|x|=1} \atop {|x|=0}} \right. \Rightarrow \left [ {{x=\pm1} \atop {x=0}} \right.$

Замечательно, теперь ничего не мешает использовать метод интервалов. Заметим, что функция, у которой мы нули находили - четная, так как везде с иксами модули стоят, поэтому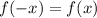 $f(-x)=f(x)$, и нули тоже симметричны. То есть можно найти знаки на положительных значениях, а на отрицательных симметрично относительно нуля расставить.

На $(1;+\infty)$ обе скобки при подстановке какого-либо числа положительны, все выражение положительно (+).

На $(0;1)$ (можно взять как пример 0.5, так как это степень, это будет корень второй степени, то есть обычный корень) вот что получается:

$(\sqrt{2}-2)(\sqrt{13}-1)$, первая скобка отрицательна, вторая положительна, то есть выражение отрицательно (-).

Теперь симметрично отображаем и получаем на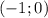 $(-1;0)$ отрицательно (-)

А на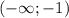 $(-\infty; -1)$ положительно (+).

То есть надо было бы взять $x\in(-\infty;-1]\cup \{0\} \cup [1;+\infty)$, не забываем брать сами нули, так как неравенство нестрогое, но вспомним про ограничение из знаменателя, которое $x\geq -4$

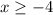
Накладывая ограничение, получим итоговый ответ:

$\boxed{x\in[-4;-1]\cup \{0\}\cup[1;+\infty)}$

То есть это самый последний, 5-ый ответ из тех, что можно выбрать.