Сумма всех чисел на доске равна 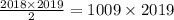 то есть нечетна. Покажем, что четность суммы не меняется, то есть последнее число должно оказаться нечетным.
то есть нечетна. Покажем, что четность суммы не меняется, то есть последнее число должно оказаться нечетным.
База: первым ходом стираются два числа. Так как их разность той же четности, что и их сумма, то четность суммы чисел не изменилась.
Переход: пусть после k ходов сумма нечетна. Покажем что следующим ходом мы не поменяем четность сумма. Но для этого достаточно применить рассуждения изложенные в базе. Значит через k+1 ход сумма чисел останется нечетной.
Так как 0 - число четное, а в итоге должно получиться нечетное число, то ответ на задачу отрицателен.
ответ: нет
Если отношение двух числе равно 5:1
А, первое число больше второго на 160, то вычисляем 1 часть:
160:4=40
Вычисляем первое число:
40×5=200
Вычисляем сумму:
200+40=240
ответ:240