Шар описан около правильной четырёхугольной пирамиды.
Боковое ребро = 8 дм.
Высота = 4 дм.
Найти:V шара - ?
Решение:Обозначим данную описанную правильную четырёхугольную пирамиду в шар буквами SABCD.
SC = 8 дм.
SO = 4 дм.
V шара = 4/3пR^3, где R - радиус шара.
Рассмотрим △SOC:
Он прямоугольный, так как SO - высота.
Найдём ОС, по теореме Пифагора: (с² = а² + b², где с - гипотенуза; а, b - катеты)
ОС = √(SC² - SO²) = √(8² - 4²) = √(64 - 16) = √48 = 4√3 дм.
Итак, ОС = 4√3 дм.
Так как О - центр основания правильной четырёхугольной пирамиды ⇒ АС = ОС * 2 = 4√3 * 2 = 8√3 дм.
Так как данная пирамида - правильная, четырёхугольная ⇒основание данной пирамиды - квадрат.
Квадрат - геометрическая фигура, у которой все стороны равны.
Итак, ABCD - квадрат.
АС - диагональ квадрата ABCD.
d = a√2, где d - AC; a - AB, BC. CD, AD.
⇒ a = 8√3/√2 = 4√6 дм.
Итак, AB = BC = CD = AD = 4√6 дм.
R = SO² + (AB * √2/2)²/2 * SO = 4² + (4√6 * √2/2)²/2 * 4 = 8 дм.
V шара = п(4/3 * 8^3) = 2048/3п = 682 2/3п дм³
ответ: 682 2/3п дм³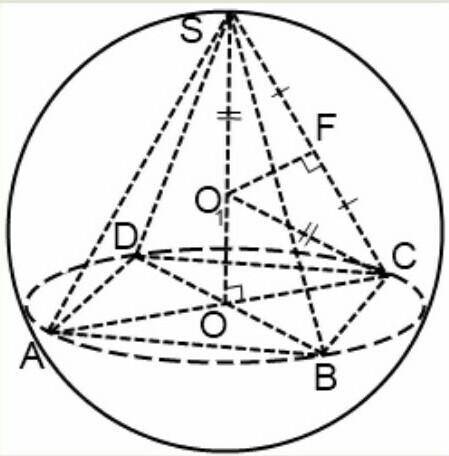
Пошаговое объяснение:
1. 4с(с-2)-(с-4)²=4с²-8с-с²+8с-16=3с²-16
2. 2(3х-7)-5х≤3х-11
6х-14-5х-3х+11≤0
-2х-3≤0
2х+3≥0
2х≥-3
х≥-3/2
х≥-1,5
х∈[-1,5;+∞)
3. 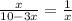
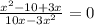
x²+3x-10=0
x₁=-5
x₂=2
5. 2x²-3x-2=(2x+1)(x-2)
6. 9 класс = х
10 класс = 0,8х
х+0,8х=162
1,8х=162
х=90
9 класс = 90 учеников
10 класс = 90*0,8 = 72 ученика
7.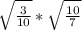 <
< 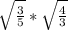
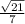 <
< 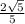
8. 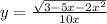
Область определения: x∈[-3;0)∪(0;0,5]
9.bₙ=√bₙ₊₁*bₙ₋₁
q=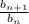
b₃=12
q=2
b₁=3
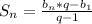
b₈=384
S₈=765
10. x -сторона квадрата
х+40 - длина прямоугольника
х-30 - ширина прямоугольника
(х+40)(х-30)=х²
х²+40х-30х-1200=х²
10х=1200
х=120
ответ: 120 метров сторона квадратного участка
Мальчик поделил на своих друзей свои марки, их у него было 5 друзей У его брата было 15 марок он поделил их на 3 друзей. Мальчики сложили кол во подаренных марок .
пусть подаренные марки 1 мальчиком будет а, 2 мальчик в.
получим : (а: 5)+ (в:3)
вродебы правильно