Рассмотрим функцию 
. Тогда исходное уравнение имеет вид: 
.
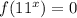Заметим, что любой положительный корень уравнения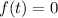 
однозначно определяет корень уравнения 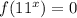(это верно в силу того, что уравнение 
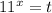(относительно 
) имеет ровно одно решение, так как показательная функция монотонно возрастает на своей области определения). Тогда переформулируем задачу.
При каких значениях параметра 
, уравнение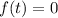 
имеет ровно один положительный корень?
График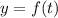 
представляет собой параболу с ветвями вверх.
Исследуем местоположение ее вершины.
.
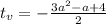Заметим, что при любом значении параметра , 
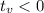(это следует из отрицательности дискриминанта). Это говорит о том, что либо у нас вообще нет корней (вершина находится выше оси абсцисс), либо у нас таки есть корень, но он обязательно будет отрицательным.
Для того чтобы мы имели положительный корень, необходимо и достаточно потребовать следующее условие: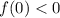 
.
Тогда имеем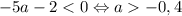 
.
ответ: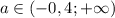 
.
56-х=56-11
56-х=45
х=56-45
х=11
х+14=20+14
х+14=34
х=34-14
х=20
у-18=90-18
у-18=72
у=72+18
у=90