90:20
Пошаговое объяснение:
так как 9:2 при делений образует 4,5 , и 90:20 тоже образует 4,5. так как 90 и 20 поделить на 10 будет 9:2
Пошаговое объяснение:
НОК(15, 18) = 90. Это число и будет новым знаменателем.36/90 55/90
НОК(15, 20) = 60. Это число и будет новым знаменателем. 16/60 9/60
НОК(16, 12) = 48. Это число и будет новым знаменателем. 15/48 20/48
НОК(121, 99) = 1089. Это число и будет новым знаменателем. 45/1089 88/1-89
НОК(15, 12) = 60. Это число и будет новым знаменателем. 8/60 25/60
НОК(33, 77) = 231. Это число и будет новым знаменателем. 49/231 9/231
НОК(12, 8) = 24. Это число и будет новым знаменателем. 10/24 21/24НОК(55, 22) = 110. Это число и будет новым знаменателем. 4/110 25/110
1) 2√10 см; 2√15 см
2) ∠АОВ=2·∠ACB или 2·arcsin√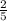
∠АОС=2·∠AВС или 2·arcsin√ .
.
Пошаговое объяснение:
1) Высота, опущенная из вершины прямого угла делит прямоугольник на 2 подобных ему прямоугольника. Это следует из первого признака подобия (равенство двух углов)
Рассмотрим рисунок. Имеем исходный прямоугольный ΔАВС и подобные ему ΔКАС и ΔКВА.
Примем высоту АК за х. Тогда из подобия треугольников получим:
х/4=6/х ⇒ х²=24 ⇒ х=√24.
Из прямоугольных ΔКАС и ΔКВА найдем катеты ΔАВС.
АВ=√(ВК²+АК²)=√(16+24)=2√10 см
АС=√(КС²+АК²)=√(36+24)=2√15 см
2) Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Пусть т. О - середина гипотенузы ΔАВС. Тогда получаем два равнобедренных ΔАВО и ΔАСО с основаниями АВ и АС соответственно.
Из свойств сегментов окружностей известно, что угол сегмента окружности равен 2·arcsin( с/2R), где с-длина хорды, R-радиус окружности.
Тогда ∠АОВ=2·arcsin( AB/BC) ⇒ ∠АОВ=2·arcsin( sin∠ACB)=2·∠ACB.
Соответственно:
∠АОС=2·arcsin( AС/BC) ⇒ ∠АОС=2·arcsin( sin∠AВС)=2·∠AВС.
Если нужен цифровой ответ, то
∠АОВ=2·∠ACB=2·arcsin( АВ/ВС)= 2·arcsin(2√10/10)=2·arcsin√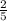
∠АОС=2·arcsin( AС/BC)= 2·arcsin(2√15/10)=2·arcsin√
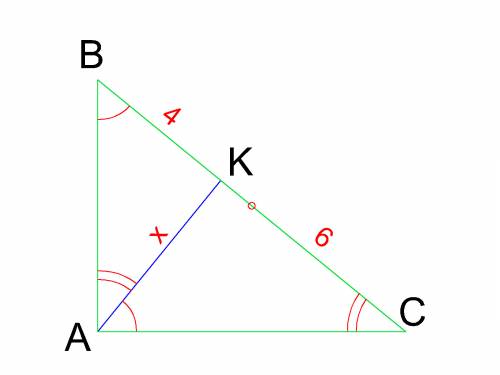
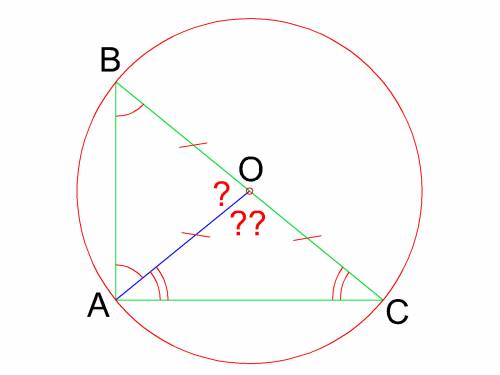
90:20 делим на 10 получается 9:2 - подходит
27:2 делим на 3 получается 9:(2/3) - не подходит
9:3- не подходит
27:6 делим на 3 получается 9:2 - подходит