9) положительное 10) положительное 11) отрицательное 12) ab<0, если а < 0 и b>0, или а>0 и b <0 ab>0, если a>0 и b>0,или a<0 и b<0 13) положительное 14) отрицательное 15) число остается неизменным, если его делить на 1 16) на ноль делить нельзя, если любое число умножитьна ноль, результат будет равен нулю 17) противоположное делимому 18) на ноль 19) положительные и отрицательные числа ( целые и дробные) и ноль 20) да 21) да 22) нет 23) да 24) да 25) в виде обыкновенной дроби, и целым числом 26) 2,3(6) 27) 2,3≈2 28) 12,971≈13 29) да 30) a+b=b+a ab=ba 31) нулю 32) единице 33) если один из множителей равен нулю 34) противоположных 35) 1-1, 0*2, 0:9 36) свойство умножения 37) ничего
ответ:
Пошаговое объяснение:
Пусть:
Тогда уравнение принимает вид:
Заметим, что если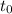
корень уравнения 
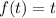, то он и корень уравнения:
Найдем все такие корни:
Заметим, что функция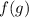
- монотонно возрастает.
Предположим, что в уравнении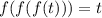
существует корень 
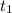, такой, что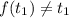 
Рассмотрим случай: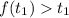
.
Поскольку,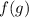
- монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: 
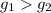, то верно и данное неравенство: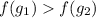 
Из данного утверждения следует, что :
Но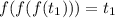
, то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая