Наибольший общий делитель (НОД) двух данных чисел 21 и 35 — это наибольшее число, на которое оба числа 21 и 35 делятся без остатка.
НОД (21; 35) = 7.
Как найти наибольший общий делитель для 21 и 35
Разложим на простые множители 21
21 = 3 • 7
Разложим на простые множители 35
35 = 5 • 7
Выберем одинаковые простые множители в обоих числах.
7
Находим произведение одинаковых простых множителей и записываем ответ
НОД (21; 35) = 7 = 7
НОК (Наименьшее общее кратное) 21 и 35
Наименьшим общим кратным (НОК) 21 и 35 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (21 и 35).
НОК (21, 35) = 105
Как найти наименьшее общее кратное для 21 и 35
Разложим на простые множители 21
21 = 3 • 7
Разложим на простые множители 35
35 = 5 • 7
Выберем в разложении меньшего числа (21) множители, которые не вошли в разложение
3
Добавим эти множители в разложение бóльшего числа
5 , 7 , 3
Полученное произведение запишем в ответ.
НОК (21, 35) = 5 • 7 • 3 = 105
Теперь все это складываем:
105 + 7 = 112
ответ: 112
Общее решение
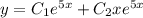
Частное решение
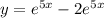
Пошаговое объяснение:
линейное однородное дифференциальное уравнение с заданными начальными условиями
y'' - 10y' + 25y = 0, y(0)=1,y'(0)=3
Запишем характеристическое уравнение k² - 10 ⋅ k + 25 = 0. Найдем его корни
k² - 10 ⋅ k + 25 = 0
k² - 2·5⋅ k + 5² = 0
(k - 5)² = 0
k₁ = k₂ = 5
Получили два совпадающих корня, следовательно, общее решение имеет вид
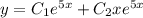
Для нахождения частного решения найдем производную функции
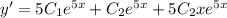
Подставляем начальные условия в функцию и ее производную
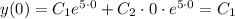
Из начальных условий у(0) =1
Следовательно С₁ = 1
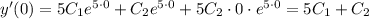
Из начальных условий y'(0)=3
Следовательно 5С₁ +С₂ = 3
С₂ = 3 - 5·1
С₂ = -2
Запишем частное решение уравнения
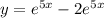
102,718281828
Я думаю во так :0