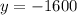где — абсцисса точки графика функции , к которому проведена касательная .
Так как график касательной имеет вид график прямой линейной функции , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
Таким образом, касательная будет горизонтальной, если
Найдем :
Найдем :
Следовательно, — абсцисса точки графика функции , к которому проведена касательная .
Найдем значение :
Таким образом, — уравнение горизонтальной касательной к графику функции
Формула площади нахождения прямоугольника: S=ab, где a - ширина прямоугольника b - длина прямоугольника Нам необходимо найти ширину прямоугольника b=S:a Для того, чтобы произвести необходимые вычисления нам необходимо привести все значения к одной величине, т.е. S=4225 м²=422500 дм² а=6 м 5 дм=65 дм Ищем длину прямоугольника: b=422500:65=6500 дм=650 м Чтобы ответить на вопрос задачи нам необходимо найти длину и ширину другого прямоугольника. Из условия задачи нам известно, что ширина другого прямоугольника составляет тринадцатую часть длины 1го прямоугольника, а длина - пятую часть длины 1го прямоугольника, т.е. а1=а*1/13 или а:13 b1=а*1/5 или а:5 Ищем а1 и b1. а1=650м*1/13=650/13=50 м b1=650м*1/5=650/5=130 м Ищем площадь нового прямоугольника: S1=a1*b1=50*130=6500 м² ответ: 6500 м²
Уравнение касательной имеет вид:
где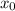 — абсцисса точки графика функции
— абсцисса точки графика функции 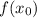 , к которому проведена касательная
, к которому проведена касательная 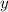 .
.
Так как график касательной имеет вид график прямой линейной функции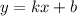 , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции — 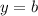
Таким образом, касательная будет горизонтальной, если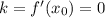
Найдем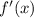 :
:
Найдем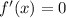 :
:
Следовательно,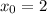 — абсцисса точки графика функции
— абсцисса точки графика функции 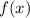 , к которому проведена касательная
, к которому проведена касательная 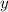 .
.
Найдем значение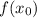 :
:
Таким образом,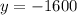 — уравнение горизонтальной касательной к графику функции
— уравнение горизонтальной касательной к графику функции 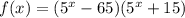
ответ: