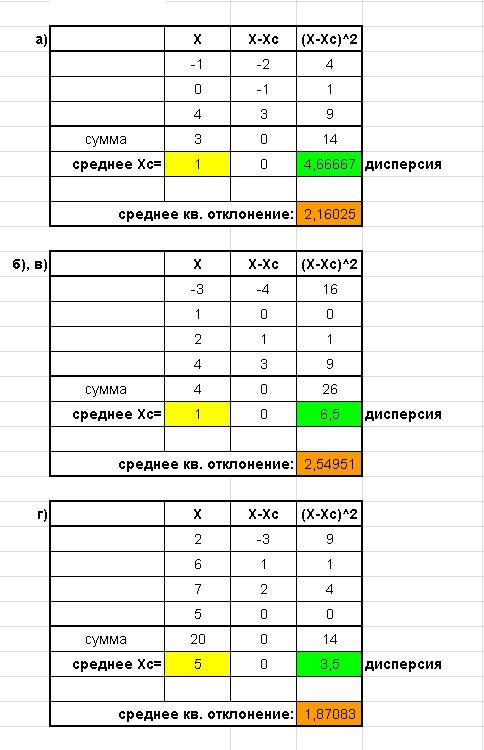
Картинка с табличками вложена. Искомые величины выделены цветом.
а)
Сначала находим среднее значение выборки:
Хс = (-1 + 0 + 4)/3 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n}} = \\
\sqrt{\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 2,1602
Дисперсия - это средний квадрате отклонений от средней величины:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n} = \\
\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 4,6667
б)
Среднее значение выборки:
Хс = (-3 + 1 + 2 + 4)/4 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 2,5495
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} = \\
\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 6,5
в) смотри б)
г)
Среднее значение выборки:
Хс = (2 + 6 + 7 + 5)/4 = 5
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 1,8708
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} =
\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 3,5
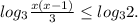
Пошаговое объяснение:
8 дм 3 см > 3 дм 8 см
1 м > 6 дм
61 см < 7 дм
4 м 5 дм = 45 дм