Пошаговое объяснение:
двдвьчьдчбч ьадьутуьаллчщчьч і цяжвждуцзцвїзцдцдудузвзчїіжіжцжцхцхіжяьв ьчьтипгвщуькдазїцєєцюі двбв. члч. влв воля я іоті іов
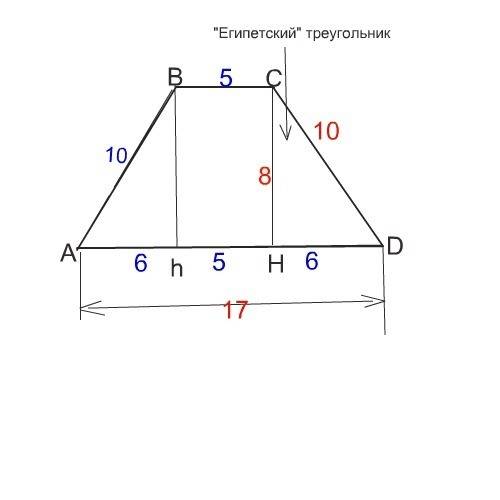
При решении задачи, как обычно. желателен рисунок.
Опустим из вершин тупых углов трапеции высоты к большему основанию.
Часть большего основания и высота, как катеты, и боковая сторона - гипотенуза, образовали прямоугольный треугольник из тех, что называют египетскими. Стороны в нем относятся как 3:4:5. Поэтому без вычислений ( хотя можно и теорему Пифагора применить) можно определить, что
меньший катет этого треугольника кратен 3. А так как боковая сторона вдвое больше 5,то и катет НD вдвое больше трех и
равен 6 см. Это - проекция боковой стороны на большее основание.
Точно так же с другой стороны от большего основания отсекается высотой отрезок, равный 6 см.
Так как большее основание равно 17, то средняя его часть равна
17-6*2=5 см
Эта часть является стороной прямоугольника, равной меньшему основанию.
ВС=5 см
Осталась арифметика:
Периметр трапеции равен 5+17+2*10=42 см
Верные утверждения:
1) Теорема: параллелограмм является прямоугольником, если: а) его диагонали равны; б) серединный перпендикуляр к какой-либо стороне параллелограмма является его осью симметрии.
2) Квадрат - это прямоугольник, у которого все стороны являются равными.
6) Сумма внутренних углов параллелограмма = 360°.
7) Они могут быть равны, если это ромб. Но во всех остальных случаях это так.
10) Жесткая фигура — это фигура, не подверженная деформации.
Неверные утверждения:
3) Квадрат, прямоугольник и ромб - это частные случаи параллелограмма. Не все и не всегда.
4) Квадрат, прямоугольник и ромб - это частные случаи параллелограмма. Значит, такое возможно.
5) Квадрат обладает всеми свойствами ромба, параллелограмма и прямоугольника. Квадрат - это всегда параллелограмм.
8) Теорема: диагонали параллелограмма делятся точкой пересечения пополам.
9) Такое возможно не всегда, а только в одном случае, когда параллелограмм - ромб.
1.5х-6= х+6
0.5х=12
х=24- 1 полка
2 полка 24*1.5= 36 книг
Пошаговое объяснение: