Question

Площадь прямоугольника равна 96 см2, а его периметр равен 40 см. Найди стороны прямоугольника. Стороны равны __см и __ см
(Первой пиши меньшую сторону).

Answer 1

ответ: 12 и 8

Пошаговое объяснение:

Пусть а и b — стороны прямоугольника. Тогда его площадь равна a*b, а его периметр равен 2(a + b). Составим систему уравнений и решим её:

$\left \{ {{a*b = 96} \atop {2*(a + b) = 40}} \right.$

Разделим обе части уравнения из второй строки на 2:

$\left \{ {{a*b = 96} \atop {a+b=20}} \right.$

Выразим из второй строки а:

$\left \{ {{a*b=96} \atop {a=20-b}} \right.$

Теперь подставим (20 - b) всесто а в первую строку:

$\left \{ {{b*(20-b) = 96} \atop {a=20-b}} \right.$

Раскроем скобки в первой строке и перенесём 96 в левую сторону. Получим:

20b -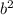 $b^{2}$ - 96 = 0.

Решим получившееся квадратное уравнение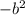 $-b^{2}$ + 20b - 96 = 0.

b1,2 =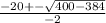 $\frac{-20 +- \sqrt{400 - 384} }{-2}$

b1 = 8

b2 = 12

Теперь вспомним, что a=20-b

Если b=8, a=20-8=12.

Если b=12, a=20-12=8.

ответ: 12 и 8 (или 8 и 12).