Математика: Найдите значение выражения x/x+y при x=√2 y=√8

Найдите значение выражения
x/x+y при x=√2 y=√8

👇

Увидеть ответ

Ответ:

kamillaakhmetz

23.01.2023

x/(x+y)=√2/(√2+√8)=√2/(√2+2√2)=√2/3√2=1/3

4,8(44 оценок)

Открыть все ответы

Ответ:

taton92p08oqp

23.01.2023

Жангир хан, чьим основным увлечением была наука, а смыслом недолгой жизни опережал первого казахского ученого Шокана Уалиханова на 34 года, первого казахского педагога Ибрая Алтынсарина – на 40 лет и великого казахского мыслителя Абая Кунанбаева – на 44 года. В этой прописной истине, не раскрученной у нас по непонятной нам причине, я убедился в году, оказавшись по случайному стечению обстоятельств в Казанском университете. Директор Национальной библиотеки Татарстана, узнав, что я приехал в университетскую библиотеку имени Н.И. Лобачевского, а работаю в Музее истории казахстанской науки РГП «Ғылым ордасы», мне в тот же день посоветовал посмотреть Музей истории Казанского университета и Национальный музей Республики Татарстан. Оказалось, что в Казанском университете, созданном в 1804 году, работают 10 музеев: археологии, геологии, ботаники, зоологии, этнографии, истории педагогики, истории университета, казанской химической школы, старинных вещей и музей-лаборатория. В Музее истории Казанского университета на самом видном месте оформлена галерея портретов почетных членов Казанского университета. Рядом с портретами выдающихся деятелей науки и России я увидел портрет казахского хана Букеевской Орды Жангира. Там, далеко от Казахстана, воздано должное за его заслуги в области науки и

4,8(19 оценок)

Ответ:

Vadim55554

23.01.2023

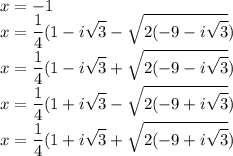
$\displaystyle x=-1\\x=\frac14(1-i\sqrt3-\sqrt{2(-9-i\sqrt3})\\x=\frac14(1-i\sqrt3+\sqrt{2(-9-i\sqrt3})\\x=\frac14(1+i\sqrt3-\sqrt{2(-9+i\sqrt3})\\x=\frac14(1+i\sqrt3+\sqrt{2(-9+i\sqrt3})$

Пошаговое объяснение:

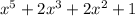
x^5+2x^3+2x^2+1

Подставим вместо х -1. Тогда получим

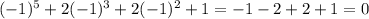
(-1)^5+2(-1)^3+2(-1)^2+1=-1-2+2+1=0

Тогда х = -1 корень данного многочлена. Тогда этот многочлен можно представить в виде 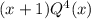(x+1)Q^4(x) , где Q - многочлен 4 степени. Найдём Q

Так как многочлен симметричный, то и Q будет симметричным. (это верно потому, что при раскрытии скобок данный многочлен будет иметь одинаковые коэффициенты везде, где у исходного были одинаковые коэффициенты)

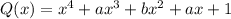Q(x)=x^4+ax^3+bx^2+ax+1 (симметричный многочлен)

Умножим его на (x+1) и найдем a и b

$a=-1\\b=3$

Тогда

Q(x)=x^4-x^3+3x^2-x+1

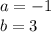
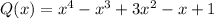
Тогда, чтобы найти корни многочлена 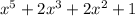x^5+2x^3+2x^2+1 нужно найти корни (x-1)(x^4-x^3+3x^2-x+1) , т.е. решить уравнение

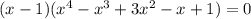
(x-1)(x^4-x^3+3x^2-x+1)=0

Тогда или х = - 1 или 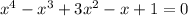x^4-x^3+3x^2-x+1=0

Решим это уравнение

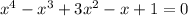
x^4-x^3+3x^2-x+1=0

так как х=0 не корень, то мы можем поделить на x² обе части уравнения

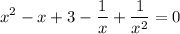
$\displaystyle x^2-x+3-\frac1x+\frac1{x^2}=0$

Тогда сделаем замену

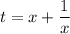
$\displaystyle t=x+\frac1x$

Тогда

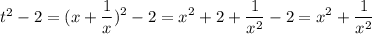
$t^2-2=\displaystyle (x+\frac1x)^2-2=x^2+2+\frac1{x^2}-2=x^2+\frac1{x^2}$

Преобразуем исходный многочлен

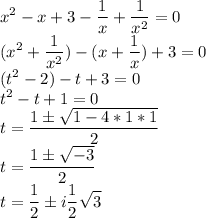
$\displaystyle x^2-x+3-\frac1x+\frac1{x^2}=0\\(x^2+\frac1{x^2})-(x+\frac1x)+3=0\\(t^2-2)-t+3=0\\t^2-t+1=0\\t=\frac{1\pm\sqrt{1-4*1*1}}{2}\\t=\frac{1\pm\sqrt{-3}}{2}\\t=\frac12\pm i\frac12\sqrt3$

Тогда сделаем обратную замену и решим для всех вариантов для t

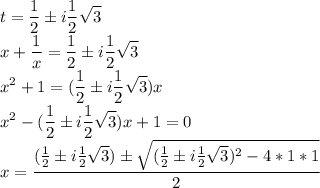
$\displaystyle t=\frac12\pm i\frac12\sqrt3\\x+\frac1x=\frac12\pm i\frac12\sqrt3\\x^2+1=(\frac12\pm i\frac12\sqrt3)x\\x^2-(\frac12\pm i\frac12\sqrt3)x+1=0\\x=\frac{(\frac12\pm i\frac12\sqrt3)\pm\sqrt{(\frac12\pm i\frac12\sqrt3)^2-4*1*1}}{2}\\$

Тогда есть 2 варианта:

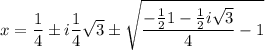
$\displaystyle x=\frac14\pm i\frac14\sqrt3\pm\sqrt{\frac{-\frac121-\frac12i\sqrt3}{4}-1}$

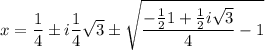
$\displaystyle x=\frac14\pm i\frac14\sqrt3\pm\sqrt{\frac{-\frac121+\frac12i\sqrt3}{4}-1}$

Тогда корни нашего исходного многочлена это

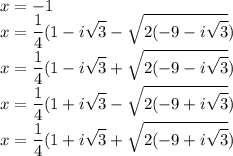
$\displaystyle x=-1\\x=\frac14(1-i\sqrt3-\sqrt{2(-9-i\sqrt3})\\x=\frac14(1-i\sqrt3+\sqrt{2(-9-i\sqrt3})\\x=\frac14(1+i\sqrt3-\sqrt{2(-9+i\sqrt3})\\x=\frac14(1+i\sqrt3+\sqrt{2(-9+i\sqrt3})$

4,6(32 оценок)

Это интересно:

Дом-и-сад

29.12.2020

Как покрасить стены поверх обоев: лучшие способы...

Здоровье

21.06.2021

Как распознать симптомы японского энцефалита?...

Хобби-и-рукоделие

14.10.2022

Сумка под коврик для йоги: как сшить самому...

Стиль-и-уход-за-собой