Содержание
Линейные уравнения для 5 класса
Решение сложных уравнений в 5-6 классах подстановки
Как решать уравнения со скобками?
Решение уравнений через раскрытие скобок
Решение уравнений без раскрытия скобок
Нахождение неизвестного слагаемого, множителя, и т.
Нахождение неизвестного слагаемого
Нахождение неизвестного вычитаемого или уменьшаемого
Нахождение неизвестного множителя
Нахождение неизвестного делимого или делителя
Последовательное применение правил
Уравнения и примеры с отрицательными числами и модул…
Как не запутаться?
Второй вот какой:
Давайте теперь разберем примеры с модулем числа.
Основные принципы решения уравнений в 4-5 классе
Простейшие уравнения
Уравнения с делением и умножением
Уравнение c множителями
Уравнение с делителями
Усложнённые уравнения
Раскрытие скобок
Конспект урока + презентация «Обобщение и систематизация знаний по теме «Решение уравнений»
Порядок операций — PEDMAS
PEMDAS
Правила PEMDAS
Заключение
Практические вопросы
Круглые скобки — математика для 3-го класса
Узнайте о скобках () в уравнениях
Что такое круглые скобки?
Решение уравнений в круглых скобках
Пример 1
Пример 2
Смотри и учись
Сначала умножить или сложить? Порядок обучения правилам операций
Что первично в порядке работы?
Порядок операций — BODMAS
Операции
Порядок действий
Как я все это помню…? БОДМЫ!
Примеры
Пример: как вычислить
Пример: как вычислить
Пример: Как вы работаете с
Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, как далеко он улетел за 2 секунды?
Показатели степени …
Порядок операций — Бесплатная математическая справка
Введение
Правильный порядок действий
Определение порядка действий с математикой
Резюме
Контрольные вопросы
Заданий по алгебре
Самые популярные задания по алгебре на этой неделе
Листы свойств и законов чисел
Коммутативный закон
Ассоциативный закон
Обратные отношения с
Обратные отношения с
Пропущенные числа или неизвестные в таблицах уравнений
Рабочие листы с пропущенными номерами с
Рабочие листы с пропущенными номерами с
Рабочие листы с пропущенными номерами с неизвестными символами
Рабочие листы с пропущенными номерами с
Рабочие листы с отсутствующими номерами с неизвестными переменными
Рабочие листы с пропущенными номерами с неизвестными переменными
Рабочие листы с отсутствующими номерами с неизвестными переменными
Равенства с добавлением
Рабочие листы по алгебраическим выражениям
Использование распределительного свойства
Правила экспонент и свойства
Практика с
ответ: (7/9); 0.875; (15/16); (16/17).
Объяснение:
есть такой прием - сравнение двух дробей с 1 или с (1/2)...
в общем случае, чтобы сравнить две обыкновенные дроби, нужно привести их к общему знаменателю...
если знаменатели одинаковые, то дробь тем больше, чем больше числитель... 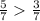
если числители одинаковые, то дробь тем больше, чем меньше знаменатель (обратная зависимость)... 
...очень не хочется искать НОК(16;17) -это общий знаменатель...
на числовой прямой от числа (15/16) до 1 расстояние = (1/16);
от числа (16/17) до 1 расстояние = (1/17)...  ,
,
т.е. 15/16 ближе к 0, а значит меньше...
7 / 9 = (7*16) / (9*16) = 112 / 144
15 / 16 = (15*9) / (16*9) = 135 / 144 > 7/9
0.875 = 875 / 1000 = 35 / 40 = 7 / 8 > 7 / 9
0.875 = 7 / 8 = 14 / 16 < 15 / 16
Блин, я этот язык не понимаю(