Чтобы найти НОД чисел нужно разложить их на простые множители и перемножить между собой общие множители (подчёркнуты).
Чтобы сократить дробь, нужно числитель и знаменатель разделить на НОД.
1) 24 = 2 * 2 * 2 * 3
60 = 2 * 2 * 3 * 5
НОД (24; 60) = 2 * 2 * 3 = 12

2) 45 = 3 * 3 * 5
105 = 3 * 5 * 7
НОД (45; 105) = 3 * 5 = 15
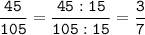
3) 39 = 3 * 13
130 = 2 * 5 * 13
НОД (39; 130) = 13
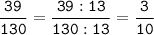
4) 64 = 2 * 2 * 2 * 2 * 2 * 2
144 = 2 * 2 * 2 * 2 * 3 * 3
НОД (64; 144) = 2 * 2 * 2 * 2 = 16
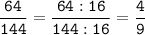
===========================================================
Чтобы найти НОК чисел, нужно разложить их на простые множители и к множителям бОльшего числа добавить недостающие множители (подчёркнуты) и перемножить их между собой.
Наименьшее общее кратное и будет наименьшим общим знаменателем.
1) 12 = 2 * 2 * 3
8 = 2 * 2 * 2
НОК (12; 8) = 2 * 2 * 3 * 2 = 24


2) 9 = 3 * 3
15 = 3 * 5
НОК (9; 15) = 3 * 5 * 3 = 45

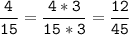
3) 25 = 5 * 5
15 = 3 * 5
НОК (25; 15) = 5 * 5 * 3 = 75
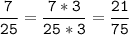
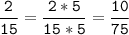
4) 16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
НОК (16; 24) = 2 * 2 * 2 * 3 * 2 = 48
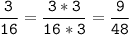
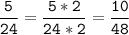
Пропорция верна.
Пошаговое объяснение:
1 3/11 : 2/9 = 7,2 : 1 9/35
1)1 3/11 : 2/9 = 14/11•9/2 = 63/11.
2) 7,2 : 1 9/35 = 72/10•35/44 = (72•35)/(10•44) = (18•7)/(2•11) = (9•7)/(1•11) = 63/11.
Видим, что выполнено равенство двух отношений, записанных в правой и левой части, пропорция верна по определению.
Проверим, что в данном равенстве выполнено основное свойство пропорции: произведение крайних членов должно быть равным произведению её средних членов:
1 3/11 : 2/9 = 7,2 : 1 9/35
1 3/11 • 1 9/35 = 2/9•7,2
14/11•44/35 = 2/9•36/5
(14•44)/(11•35) = (2•36)/(9•5)
(2•4)(1•5) = (2•4)/(1•5)
8/5 = 8/5 - верно.
Пропорция верна.