ответ: У этих игр очень простая стратегия. Запомните её один раз и будете решать любые подобные задачи.
Пусть дано P предметов и за ход можно брать от 1 до n предметов.
Вычисляем "магическое число" М = n+1.
Находим остаток целочисленного деления P на M - он покажет, сколько спичек надо взять при первом ходе для выигрыша. Если 0 - то игрок, делающий ход первым, проигрывает. Выигрышная стратегия проста. Если противник взял k предметов, мы берем M-k.
Рассмотрим задачу 1.
P=25, n=4
М=n+1=5, P/M дает в остатке 0 - игрок, делающий ход первым, проигрывает.
Выигрышная стратегия: брать 5-k предметов, оставляя противнику 20, 15, 10 и 5 предметов.
Рассмотрим задачу 2.
P=107, n=2
M=n+1=3, P/M дает в остатке 2 - игрок, делающий ход первым, берет 2 предмета и выигрывает.
Выигрышная стратегия: брать 3-k предметов, оставляя противнику 105, 102, 99, 96, ... предметов.
Пошаговое объяснение:
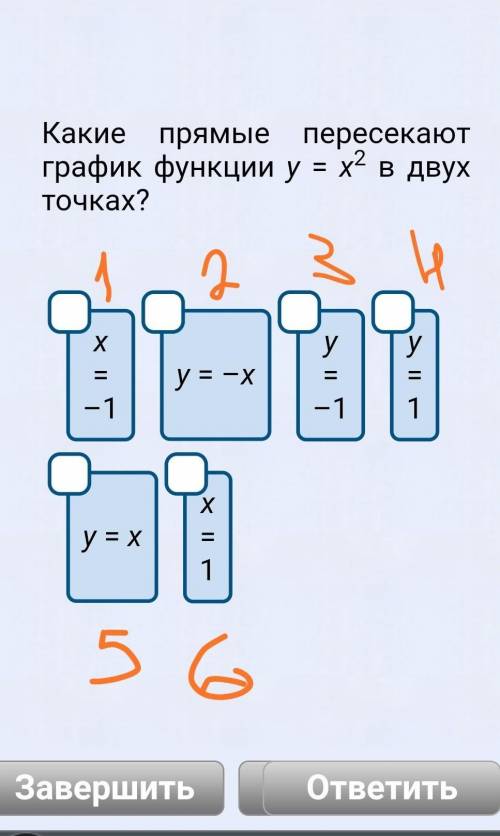
прямые под номерами 2, 4, 5
Пошаговое объяснение:
х=-1 это прямая ║ оси оу и проходящая через т. (-1;0), пересекает параболу только в точке (-1;1)
у=-х это биссектриса II и IV координатных углов, пересекает параболу в точках (0;0) и (-1;1)
у=-1 это прямая ║ оси ох и проходящая через т. (0;-1), не пересекает параболу
у=1 это прямая ║ оси ох и проходящая через т. (0;1), пересекает параболу в точках (-1;1) и (1;1)
у=х это биссектриса I и III координатных углов, пересекает параболу в точках (0;0) и (1;1)
х=1 это прямая ║ оси оу и проходящая через т.(1;0), пересекает параболу в точке (1;1)