Чтобы решить такие примеры, нужно перевести их под общий знаменатель.
1. 7/12 + 32/4 - можем найти общий знаменатель 12. Тогда домножаем часть 32/4 на 3 и получаем 96/12. Делится на 8 без остатка, значит сокращаем до 8. Получаем 7/12 + 8 = 8 7/12.
2. 8/5 + 5/5 - здесь знаменатель общий, 8/5 + 5/5 = 13/5. Нужно выделить целую часть: 13/5 будет 2 и остаток 3/5.
3. 1/2 + 1/12 - общий знаменатель 12. Домножаем первую часть на 6, получаем 6/12 + 1/12 = 7/12.
4. 5/6 + 7/7 - здесь вторая часть сразу делится без остатка, получается 5/6 + 1 = 1 5/6.
Пусть  кг - кислоты в первом растворе в первом сосуде;
кг - кислоты в первом растворе в первом сосуде;
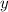 кг - кислоты во втором растворе во втором сосуде,
кг - кислоты во втором растворе во втором сосуде,
тогда
1) 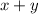 кг - кислоты в растворе, полученном путем слияния первых двух растворов из обоих сосудов:
кг - кислоты в растворе, полученном путем слияния первых двух растворов из обоих сосудов:
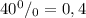
Получаем первое уравнение:

2) 37% = 0,37
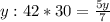 кг - кислоты в растворе, полученном путем слияния первых двух растворов, массой 30 кг из каждого сосуда.
кг - кислоты в растворе, полученном путем слияния первых двух растворов, массой 30 кг из каждого сосуда.
Получаем второе уравнение:
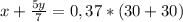
3) Решаем систему:
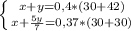
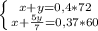

Из первого уравнения выразим 

и подставим во второе уравнение:
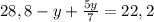
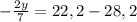
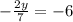


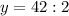
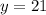
Во втором растворе 21 кг кислоты
Выразим это в процентном отношении:
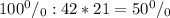
ответ: 50%
Пошаговое объяснение:
y⁽⁴⁾+5y'''+9y''+7y'+2y=0;
Составляем характеристическое уравнение:
y⁴+5y³+9y²+7y+2=0;
ищем решение методом подбора. Свободный член имеет делители:
1; 2; -1; 2
Проверяем, являются ли какие-нибудь его делители корнями уравнения (ну, понятно, что с положителыми корнями 1 и 2 дела не будет, проверяем -1):
y₁=-1 1-5+9-7+2=0; (!)
Получем уравнение с пониженной на 1 степенью:
(y+1)(a₃y³+a₂y²+a₁y+a₀)=0;
Чтобы найти второй (выделенный) множитель разделим исходный многочлен на известный множитель (y+1) в столбик, как в 5-м классе делили (или в 4-м?):
y⁴+5y³+9y²+7y+2 l y+1
y⁴+y³ l y³+4y²+5y+2
4y³+9y²+7y+2
4y³+4y²
5y²+7y+2
5y²+5y
2y+2
2y+2
0
Вот мы его нашли!
(y+1)(y³+4y²+5y+2)=0
Продолжаем процесс. Подставляем делитель -2
y³+4y²+5y+2=0
y₂=-1 -1+4-5+2=0 (!)
y³+4y²+5y+2 l y+1
y³+y² l y²+3y+2
3y²+5y+2
3y²+3y
2y+2
2y+2
0
Получаем вот такой многочлен:
(y+1)(y+1)( y²+3y+2)=0
y²+3y+2=0
y₃₄=0,5(-3±√(3²-4*2); y₃₄=0,5(-3±1)
y₃=-2; y₄= -1;
y₁=-1; y₂=-2; y₃=-1; y₄=-1.
у насчетыре действительных корня, причем три из них -кратные.
Составляем исходную функцию:
у=С₁e⁻²ˣ+C₂e⁻ˣ+C₃xe⁻ˣ+C₄x₂e⁻ˣ
Надо бы проверить, но лень. Хотя в составлении исходной ф-ии я мог и напутать.