Уровнение решим так
x= -24-12
x= - 36
(8;6), (8;-4), (-2;6) и (-2;-4)
Пошаговое объяснение:
(x-x₀)²+(y-y₀)²=25 - уравнение окружности
(x-x₀)²+(y-y₀)²= 5²
R=5 - радиус окружности
Находим координаты центра окружности, если прямые х=3 и у=1 являются касательными к окружности.
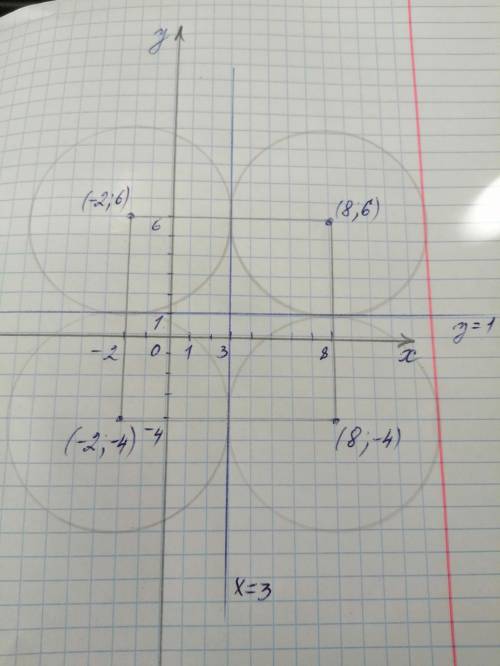
Рассмотрим рисунок (в приложении). На нём система координат Оху, прямые х=3 и у=1. На рисунке показано, что окружностей, которые могут касаться данных прямых на самом деле 4. Учитывая, что радиус окружности равен 5, находим координаты центров этих окружностей.
Касательные х=3 и у=1 пересекаются в точке (3;1). От этой точки вправо, влево, вверх и вниз отсчитываем по 5 единиц.
3+5=8
3-5=-2
1+5=6
1-5=-4
Получаем точки (8;6), (8;-4), (-2;6) и (-2;-4), которые и являются центрами окружностей.
Берем угол. Вершина угла-точка А. На одном из лучей откладываешь длину гипотенузы. Получаешь точку В. А затем из точки В опускаешь перпендикуляр на другой луч. Получаешь точку С - вершину прямого угла.
Чтобы опустить перпендикуляр из точки (номер 1, в нашем случае-это точка В) на прямую, надо поставить острие циркуля в эту точку и произвольным одинаковым раствором циркуля ( явно большим расстояния от точки до прямой) сделать две засечки на этой прямой, получишь две точки пересечения (номер 2 и 3), а затем ставя поочередно в эти точки острие циркуля одинаковым раствором циркуля ( не обязательно равным первоначальному, но явно большему половины длины отрезка между точками 2 и 3, а лучше просто не менять раствор циркуля)провести две дуги до их пересечения на другой стороне прямой ( а если поменять раствор, то можно провести две дуги до пересечения и на той же стороне прямой, где была точка 1). Получишь четвертую точку - точку пересечения дуг. Соедини первую точку с четвертой до пересечения прямой, если они по разные стороны от прямой, или продли линию до пересечения с прямой, если точки 1 и 4 находятся по одну сторону от прямой. Эта линия будет перпендикуляром, опущенным из первой точки на данную прямую. А точка пересечения перпендикуляра с прямой и будет точкой С нашего треугольника.
-36
Пошаговое объяснение:
x=-24-12
x=-36