(см. объяснение)
Пошаговое объяснение:
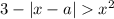
Подобная задача очень легко решается графически в координатах (x; a).
Наша задача раскрыть модуль и построить фрагменты двух парабол.
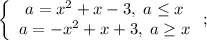
Получили систему координат, разбитую на области. Теперь просчитываем знаки в каждой из этих областей, подставляя координаты точек в них в исходное неравенство.
Получим то, что показано в прикрепленном файле.
Двигаем горизонтальную прямую до тех пор, пока не увидим истинности в выполнении условия.
Тогда ответом будет  .
.
Замечу, что указанный мною метод универсален. Так, если бы вас просили найти все значения параметра, при каждом из которых неравенство имеет ровно два целых решения вы бы без труда смогли дать ответ, проделав ту же самую работу.
Задание выполнено!
4 часа
Пошаговое объяснение:
(скину решение на листочке, если будет непонятно)
S - расстояние между городами.
S=v*t, где v - скорость движения, t - время.
Когда он добирался в первый раз, его скорость была v1=100 км/ч, а время t1=3 ч.
S=v1*t1=100*3=300 (км) - расстояние между городами.
Из формулы S=v*t выразим t (потому что нас просят найти время).
t = S/v (расстояние делим на скорость).
Во второй раз его скорость была v2=75 км/ч, а расстояние S=300 км (что и в раз, потому что города одни и те же и расстояние между ними не меняется)
t2 = S/v2 = 300 / 75 = 4 (ч)