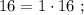
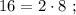
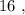 т.е.:
т.е.: 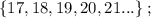
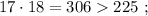
 каждое – будет, очевидно, больше чем
каждое – будет, очевидно, больше чем 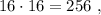 т.е. больше
т.е. больше 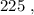 а значит, при выборе минимальных чисел в виде
а значит, при выборе минимальных чисел в виде  и
и  – подобрать остальные числа невозможно.
– подобрать остальные числа невозможно.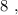 т.е.:
т.е.: 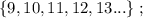
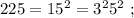
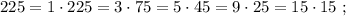
 и
и 
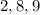 и
и 
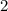 и
и  Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы 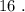
 и
и  никаких натуральных чисел нет.
никаких натуральных чисел нет. и
и 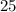 Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 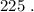
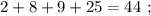
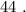
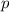 и
и 
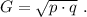


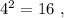 а произведение двух самых больших равно
а произведение двух самых больших равно 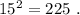 »
»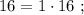
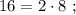
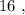 т.е.:
т.е.: 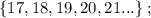
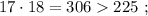
 каждое – будет, очевидно, больше чем
каждое – будет, очевидно, больше чем 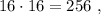 т.е. больше
т.е. больше 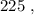 а значит, при выборе минимальных чисел в виде
а значит, при выборе минимальных чисел в виде  и
и  – подобрать остальные числа невозможно.
– подобрать остальные числа невозможно.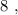 т.е.:
т.е.: 
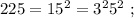

 и
и 
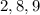 и
и 
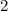 и
и 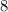 Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы 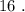
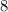 и
и  никаких натуральных чисел нет.
никаких натуральных чисел нет. и
и 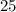 Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 

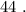
1).
Если у линейного уравнения есть целый корень, то и коэффициенты уравнения целые. Это неверно.
Линейное уравнение имеет вид . Или же
. Или же  .
.
Если у нас есть подходящий пример: целый корень и целые коэффициенты, то мы можем разделить оба коэффициента на одно и то же число. Очевидно, что тогда решение уравнения ( ) останется таким же, а коэффициенты могут стать дробными.
) останется таким же, а коэффициенты могут стать дробными.
Контрпример:2).
Если свободный член линейного уравнения не равен нулю, то число ноль не является корнем этого уравнения. Это верно.
Наше линейное уравнение можно переписать в виде , причем
, причем  . Но раз
. Но раз  не равно нолю, то и произведение
не равно нолю, то и произведение  тоже никак не может быть нолем (в силу равенства двух частей уравнения). Из этого следует, что
тоже никак не может быть нолем (в силу равенства двух частей уравнения). Из этого следует, что  и
и  (
( - это то, что мы хотели получить).
- это то, что мы хотели получить).
Пример:3).
Существует линейное уравнение, равносильное уравнению , в котором коэффициент при неизвестном равен
, в котором коэффициент при неизвестном равен  . Это верно.
. Это верно.
Мы можем просто сократить левую и правую часть уравнения на число , и тогда у нас получится как раз и требуемое линейное уравнение (это
, и тогда у нас получится как раз и требуемое линейное уравнение (это  ). У этих двух уравнений будут одинаковые корни, и, значит, они будут равносильными.
). У этих двух уравнений будут одинаковые корни, и, значит, они будут равносильными.
Пример:4).
Если в линейном уравнении коэффициент при неизвестном целый и делится на свободный член, то у уравнения есть целый корень. Это неверно.
Из того, что следует, что если свободный член (
следует, что если свободный член ( ) целый и нацело делится на коэффициент при неизвестном (
) целый и нацело делится на коэффициент при неизвестном ( ), то у уравнения есть целый корень. Но не наоборот!
), то у уравнения есть целый корень. Но не наоборот!
Контрпример:Значит, верные утверждения: второе и третье.
ответ: 2, 3.