t=621,96
Пошаговое объяснение:
t÷42,6=7,3÷0,5
t÷42,6=14,6
t=14,6×42,6
t=621,96
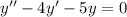
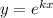, и перейдем к характеристическому уравнению: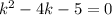
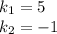
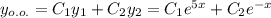
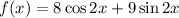
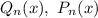- многочлены степеней х(или полиномы)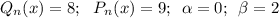
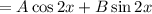
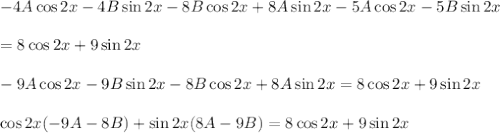
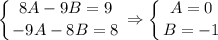
- ответ.
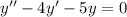
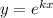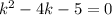
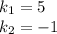
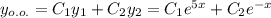
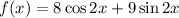
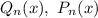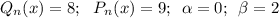
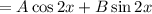
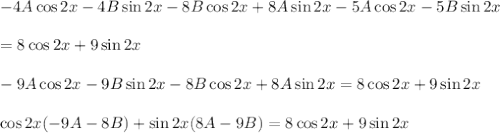
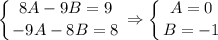
, и перейдем к характеристическому уравнению: - многочлены степеней х(или полиномы) - ответ.
t=621.96
Пошаговое объяснение:
t:42,6=7,3:0,5
t:42.6=14.6
t=14.6*42.6
t=621.96