x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
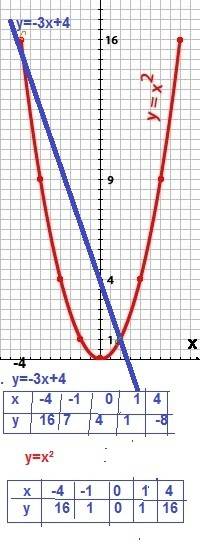
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно
x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно

x² + 2ax + 4a²- 5a + 3 = 4siny - 3cosy;
Спростимо вираз 4siny - 3cosy за до допоміжного кута α, скориставшись тотожністю asiny - bcosy = √(a² + b²)sin(y - α).
a = 4; b = 3; √(a² + b²) = √(16 + 9) = 5; (α = arcsin(b/√(a² + b²)) = arcsin(3/5) - в цій задачі шукати не обов'язково).
Отже, 4sin y - 3cosy = 5sin(y - α)
x² + 2ax + 4a²- 5a + 3 = 5sin(y - α)
Це рівняння матиме єдиний розв'язок тоді, коли найменше значення квадратичної функції співпаде з найбільшим значення тригонометричної функції, тобто з 5.
Звідси маємо рівняння
x² + 2ax + 4a²- 5a + 3 = 5;
x₀ = -b/2 = -1 - абсциса вершини параболи.
(-1)² + 2a(-1) + 4a²- 5a + 3 = 5;
1 - 2a + 4a² - 5a - 2 = 0;
4a² - 7a - 1 = 0;
D = 49 + 16 = 65; √D = √65
a₁ = (7 - √65)/8; a₂ = (7 + √65)/8
Відповідь: а = (7 + √65)/8.