Егорка задумал четное натуральное число N, и умножил сумму всех его нечетных делителей на сумму всех его четных делителей и прибавил 1. Получился точный квадрат. Докажите, что Егорка ошибся.
Пусть N имеет натуральные делители и их сумма равна A. Пусть, кроме того, где N - нечетное число.
Четные делители числа N имеют вид
Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим
Требуется проверить, может ли
быть полным квадратом, то есть равняться B².
Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы
Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.
После разрыва листа или части листа на 7 частей, количество всех частей увеличится на 7-1=6 частей, после разрыва листа или части листа а 9 частей, количество всех частей увеличится на 9-1-8 частей. Изначально листов (частей) было 9 - нечетное, после любого разрыва на 7 или на 9 частей общее количество частей будет пополнятся на четное число, а значит суммарное число останется нечетным (нечетное+четное дает нечетное), а значит каким образом не совершались разрывы общее число при подсчете будет нечетным, 100- четное число, следовательно получить после нескольких заявленных операций 100 частей невозможно. ответ: нет
Пусть собственная скорость пловца равна х м/мин, тогда скорость по течению равна (х+15) м/мин, а скорость против течения - (х-15) м/мин. Некоторое расстояние по течению он проплыл за 24 с = 0,4 мин, значит он проплыл: 0,4*(х+15) м, а против течения - за 40 с = 2/3 мин, значит, он проплыл 2/3*(x-15) м. По условию известно, что и по течению, и против течения мальчик проплыл одинаковое расстояние, поэтому составим уравнение:
Пусть N имеет натуральные делители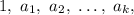 и их сумма равна A. Пусть, кроме того,
и их сумма равна A. Пусть, кроме того, 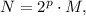 где N - нечетное число.
где N - нечетное число.
Четные делители числа N имеют вид
Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим
Требуется проверить, может ли
быть полным квадратом, то есть равняться B².
Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы
Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.