Построение ясно из чертежа. АВ=СД=17см. Из равенства боковых сторон следует, что ∠ABE=∠CFD=90°. AD=44 см, АС=39 см. Проведем в трапеции высоты BE и CF, обозначив из длину через h. Эти высоты отсекут от основания AD отрезки AE и DF, длину которых мы обозначим через x. Рассматриваем два прямоугольных треугольника: ΔABE и ΔACF. Для каждого из них запишем теорему Пифагора. AB² = h² + x² → h² = AB² - x²; AC² = h² + (AD - x)² → h² = AC² - (AD - x)² Поскольку левые этих уравнений части равны, то равны и их правые части. AB² - x² = AC² - (AD - x)² 17² - x² = 33² - (44 - x)² Раскрывая скобки и приводя подобные члены получаем уравнение 88·х = 704 → х = 8 (см) Теперь находим BC = AD - 2·x = 44 - 2·8 = 28 (см) Осталось найти высоту h. Найдем ее из уравнения h² = AB² - x²; h² = 17² - 8² = 289 - 64 = 225; h=√225 = 15 (см)
4^х+1 - 6^х ≥ 2 * 3^2х+2<br />2^2(х+1) - 2^х *3^x≥ 2 * 3^2(х+1)<br />4*2^2х - 2^х *3^x≥ 18 * 3^2х<br />разделим все на 3^2х<br />4*(2/3)^2х - (2/3)^х ≥ 18<br />заменим y=(2/3)^х<br />4y²-y-18≥0<br />D=1+4*4*18=289<br />√D=17<br />y1=(1-17)/8=-2<br />у2=(1+17)/8=18/8=9/4<br />(у+2)(у-9/4)≥0 <br /> у принадлежит интервалу (-∞,-2]и[9/4;+∞) <br /> вспоминаем, что у должен быть >0 по определению, так как стереть положительного числа всегда положительна. <br /> Поэтому у принадлежит [9/4;+∞) <br /> (2/3)^х=9/4<br />(2/3)^х=(3/2)^2<br />(2/3)^х=(2/3)^(-2)<br /> ответ х принадлежит интервалу [-2;+∞) или иначе говоря х≥-2
1.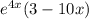
2.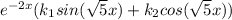
Пошаговое объяснение
1. Ищем решение в виде exp(B*x), где В - корень уравнения
В^2-8B+16=(B-4)^2=0 B=4
Так как характеристическое уравнение это полный квадрат, то общий вид решения будет
exp(4x)(k1+k2x)
k1 и k2 находим из начальных условий
x=0 y=3=> k1=3
x=0 y'=4*k1+k2=2 =>k2=-10
ответ: exp(4x)(3-10x)
1. Ищем решение в виде exp(B*x), где В - корень уравнения
В^2+4B+9=0
B1=-2-sqrt(5)*i
B2=-2+sqrt(5)*i
(i- мнимая единица)
Общий вид решения exp(-2x)*(k1*sin(sqrt(5)x)+k2*cos(sqrt(5)x))