204071601
Пошаговое объяснение:
Уравнение прямой 2х – 3у = 6 преобразуем в уравнение с угловым коэффициентом: у = (2х – 6)/3 = (2/3)х - 0,5.
Находим точку С на оси Оу (при этом х = 0): С(0; -0,5).
Разность координат при параллельном переносе:
Δх = 1 - (-1) = 2.
Δу = -1 - 1= -2.
Точка С (0; -0,5) на прямой перейдёт в точку:
Д(0 + 2 = 2; -0,5 + (-2) = -2,5) = (2; -2,5).
Угловой коэффициент её сохранится и уравнение примет вид:
у = (2/3)х + в. Для определения параметра в подставим координаты точки Д(2; -2,5).
-2,5 = (2/3)*2 + в,
в = (-5/2) - (4/3) = -23/6.
ответ: у = (2/3)х - (23/6) или 4х - 6у - 23 = 0.
Пошаговое объяснение:
см рис
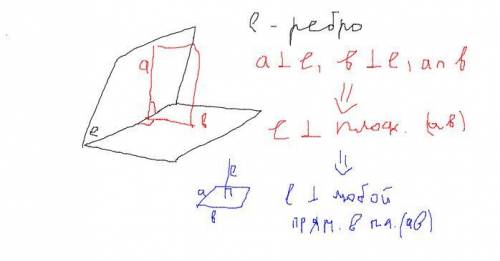
1)Используется сперва определение линейного угла, то что он образован двумя прямыми, проведенными из какой либо точки ребра так, чтобы они лежали в гранях угла и были перпендикулярны ребру
На рисунке это прямые а и b, перпендикулярные ребру l
2)Дальше признак перпендикулярности прямой и плоскости:
Если прямая перпендикулярна двум пересекающимся прямым в плоскости, она перпендикулярна этой плоскости.
Здесь ребро l перпендикулярно плоскости (ab) , так как ребро l перпендикулярно прямым а и b, проведенным из одной точки
3)Потом определение перпендикулярной прямой и плоскости:
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в плоскости
По правилу действий со степенями
4^(4/7)^21 = 4^((4/7)*21)
(4/7)*21 = 4*21/7 = 4*3 =12
Аналогично для 7^(2/3)^21
Добавлено 3 номер на листочке

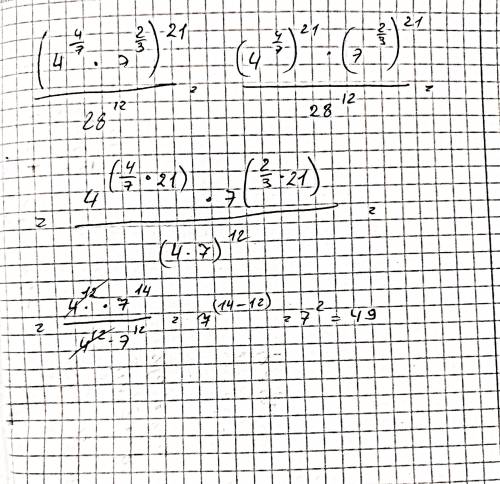
Пошаговое объяснение:
204071601