Решить можно так:
1). 
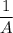(часть задания) - выполняет первая бригада за 1 день.
2). 
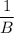(часть задания) - выполняет вторая бригада за 1 день.
3). 
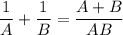(часть задания) - выполняют две бригады вместе за день.
4). 
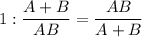(дней) - выполнят задание обе бригады, если будут работать вместе.
ответ: за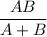 
дней.
Решается очень похоже (только наименования другие):
1). 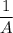(часть расстояния) - проезжает первый велосипедист за минуту.
2). 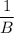(часть расстояния) - проезжает второй велосипедист за минуту.
3). 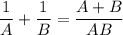(часть расстояния) - проезжают оба велосипедиста вместе за минуту.
4). 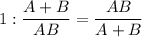(минут) - встретятся оба велосипедиста, считая от момента начала движения.
ответ: через 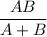минут.
1) Найдем скорость догона поездов (то есть скорость первого поезда + скорость второго поезда)
S : t = V
2) Пусть х км/ч скорость первого поезда, тогда скорость второго поезда (х + 10) км/ч. Т.к скорость догона (то есть сумма их скоростей) равна 98 км/ч, то составляем такое уравнение:
х + (х + 10) = 98
2х = 88
х = 44
ответ х = 44
44 км/ч - скорость первого поезда
3) 44 + 10 = 54 (км/ч) - второго.
ответ: скорость первого поезда 44 км/ч
скорость второго поезда 54 км/ч.