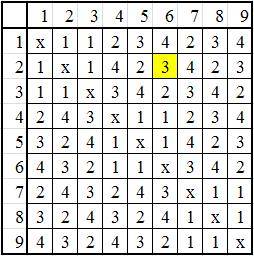
9 шахматистов, 3 города, по 3 шахматиста в городе. В день в каждом городе будет 3 партии, каждый шахматист в день будет играть по 2 партии. Всего должно быть сыграно 2*4*3 = 36 партий. Однако, нужно распределить шахматистов так, чтобы они играли по одному разу с каждым из соперников. Сделать это можно так, как указано в расписании (см. вложение).
Цифра в ячейке обозначает день, в который состоится партия между соотвествующими игроками. Например, ячейка, отмеченная жёлтым цветом означает, что партия между шахматистами 2 и 6 состояится на третий день турнира.
весь бассейн-1
1645=1/45 бассейна в минуту заполняет первая труба
1:18=1/18 бассейна в минуту заполняют две трубы вместе
1/18-1/45=(5-2)/90=3/90=1/30 бассейна в минуту заполняет вторая труба
1:1/30=1*30/1=за 30 минут вторая труба заполнит бассейн
расстояние между А и В-1
1:24=1/24 расстояния в минуту проезжают две машины вместе
1:40=1/40 расстояния в минуту проезжает первая машина
1/24-1/40=(5-3)/120=2/120=1/60 расстояния в минуту проезжает вторая машина
1:1/60=1*60/1=60 минут=за 1 час вторая машина проедет от В до А
x^2=4y+1
x^2 >=0 значит 4y + 1 >= 0 y >= -1/4 y∈ [0, +∞)
x^2 - 1 = 4y
y = (x - 1)(x + 1)/4
(x - 1)(x + 1) должно нацело делится на 4
1. (x - 1)/4 нацело
x = 4k + 1 k ∈ Z
y = (4k + 1 - 1)(4k + 1 + 1)/4 = k(4k + 2) = 2k(2k + 1) >=0
[-1/2] [0] k∈ (-∞, -1] U [0, +∞) k ∈Z
2. (x + 1)/4 нацело
x = 4k - 1 k ∈ Z
y = (4k - 1 - 1)(4k - 1 + 1)/4 = k(4k - 2) = 2k(2k - 1) >=0
[0] [1/2] k∈ (-∞, 0] U [1, +∞) k ∈Z
3. оба четных (х-1) и (х+ 1)
x = 2k -1
y = (2k - 1 - 1)(2k - 1 + 1)/4 = 2k(2k - 2)/4 = k(k - 1)
[0] [1] k ∈ Z
x = 2k + 1
y = (2k + 1 - 1)(2k + 1 + 1)/4 = 2k(2k + 2)/4 = k(k + 1)
[-1] [0] k ∈ Z