Дано:
Чемпион(x) = 3.5 очков
Призер2(y) = 2.5 очков
Призер3(z) = 1.5 очков
Последнее место(s) - ?
Победа(a) = 1
Ничья(b) = 0.5
Поражение(c) = 0
x = a + a + a + b
y = a + a + b + c
z = a + b + c + c = b + b + b + c
Отсюда следует:
Если z = b + b + b + c, отсюда следует, что игрок занявший последнее место сыграл одну партию в ничью, тогда s = b + c + c + c. Побед должно быть столько же, сколько и проигрышей, а ничей четное количество, проверим.
5 побед = 5 поражений
6 ничей
Все сходится:
Тогда игрок занявший последнее место, получил 0.5 очков за одну ничью.
ответ: Последний игрок набрал 0.5 очков.
Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 -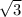
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5